Автор: Денис Аветисян
Новое исследование показывает, как скалярные поля вокруг формирующихся чёрных дыр генерируют мощные сигналы, потенциально обнаружимые гравитационно-волновыми детекторами.
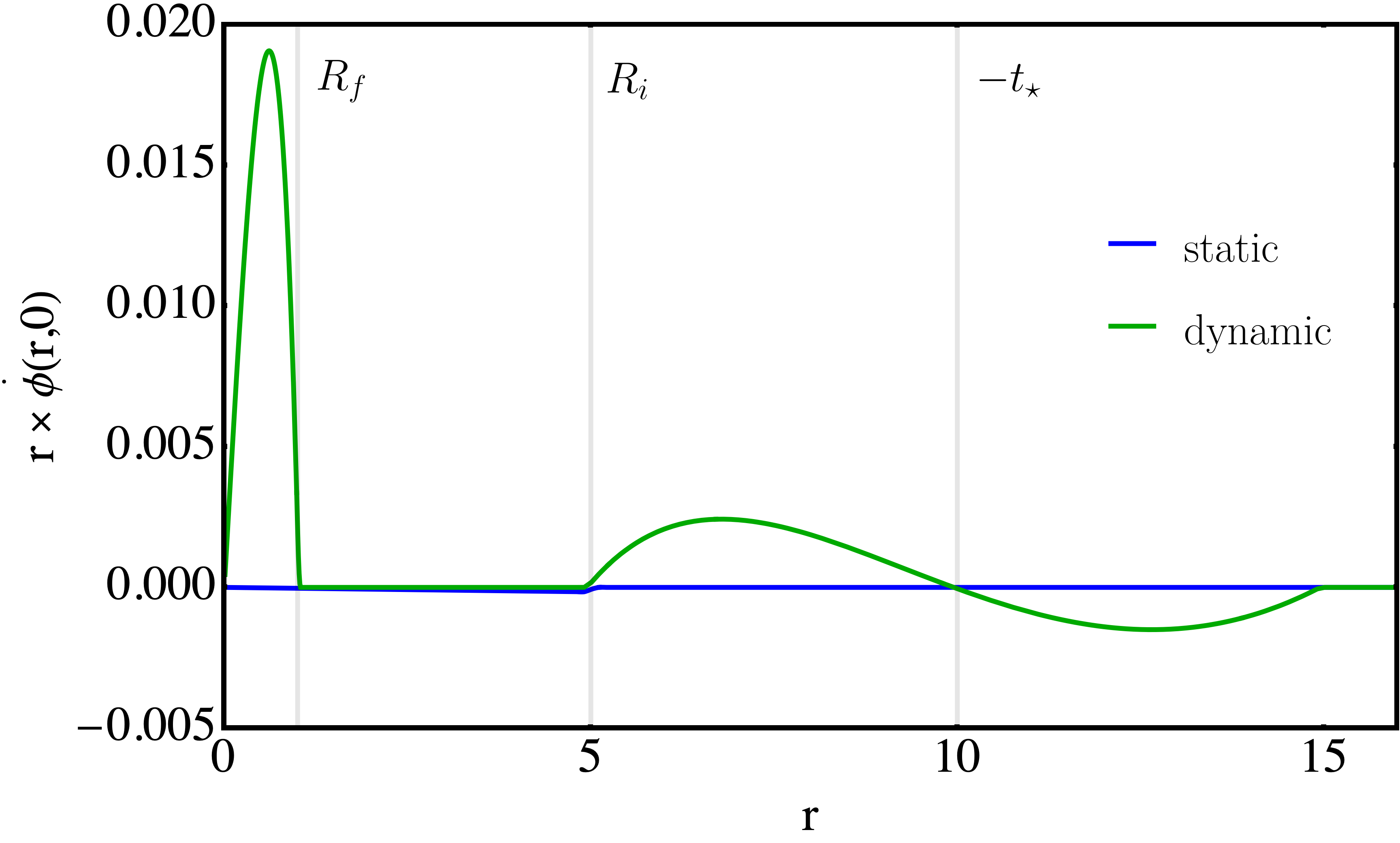
Работа посвящена анализу эволюции скалярных полей при коллапсе материи в чёрную дыру и спектральным характеристикам возникающих при этом транзиентных сигналов.
Формирование черных дыр, сопровождающееся коллапсом массивных звезд, может высвобождать энергию, заключенную в окружающих скалярных полях. В работе ‘Scalar Tsunamis from Black Hole Formation’ проведено углубленное исследование эволюции этих полей, учитывающее эффекты общей теории относительности и уточненные начальные условия. Показано, что спектральные характеристики и общая энергия высвобождаемого «скалярного цунами» существенно зависят от исходной конфигурации поля, оставаясь сопоставимой с оценками в плоском пространстве. Может ли детальное моделирование подобных событий привести к обнаружению новых, слабозаметных сигналов, свидетельствующих о формировании черных дыр во Вселенной?
Поиск сигналов в гравитационном танце: Начало пути
Поиск новых элементарных частиц часто базируется на регистрации кратковременных сигналов, возникающих при астрофизических событиях, таких как вспышки сверхновых. Именно поэтому понимание механизмов распространения этих сигналов в космическом пространстве имеет первостепенное значение. Задержки, искажения и ослабление сигнала по мере его продвижения к наблюдателю могут существенно повлиять на интерпретацию данных и выявление новых частиц. Точное моделирование распространения сигналов, учитывающее различные факторы, включая межзвездную среду и гравитационные эффекты, необходимо для повышения точности и надежности поисков, а также для извлечения максимальной информации из редких и ценных астрофизических событий.
Скалярные поля, являющиеся фундаментальными элементами множества теоретических моделей, представляют собой перспективные кандидаты на роль носителей сигналов, возникающих при астрофизических событиях. Однако, их поведение вблизи черных дыр характеризуется значительной сложностью. Интенсивная гравитация, создаваемая этими объектами, оказывает существенное влияние на динамику скалярных полей, приводя к различным эффектам, таким как флуктуации, резонансы и излучение \text{Hawking}. Моделирование этого взаимодействия требует учета искривления пространства-времени и использования сложных математических методов для точного предсказания эволюции поля. Понимание этих процессов критически важно для интерпретации сигналов, регистрируемых современными астрофизическими обсерваториями, и для проверки предсказаний различных теоретических моделей, включая теории темной материи и модифицированной гравитации.
Для всестороннего изучения взаимодействия скалярных полей с экстремальной гравитацией чёрных дыр необходимы сложные модели, учитывающие искривление пространства-времени. Эти модели, основанные на решениях уравнений Эйнштейна, позволяют отследить эволюцию поля вблизи горизонта событий, выявляя такие эффекты, как усиление сигнала или формирование специфических резонансов. \nabla_{\mu} \phi \nabla^{\mu} \phi — это лишь один из примеров математических выражений, описывающих динамику скалярного поля φ в искривленном пространстве. Точное моделирование требует численных методов и глубокого понимания общей теории относительности, поскольку даже незначительные отклонения в геометрии пространства-времени могут существенно повлиять на поведение поля и, следовательно, на наблюдаемые астрофизические сигналы.
Моделируя искривление: Численные методы познания
Для моделирования динамики скалярных полей в гравитационном поле чёрной дыры используются численные симуляции, основанные на метрике Шварцшильда. Эти симуляции позволяют исследовать эволюцию поля во времени, начиная с заданной начальной конфигурации. Решение уравнений движения, описывающих поведение поля в искривленном пространстве-времени, производится численно на дискретной сетке. В качестве базовой метрики используется метрика Шварцшильда ds^2 = -(1 - \frac{2GM}{rc^2})c^2dt^2 + (1 - \frac{2GM}{rc^2})^{-1}dr^2 + r^2(d\theta^2 + sin^2\theta d\phi^2), описывающая геометрию пространства-времени вокруг невращающейся сферически симметричной массы M. Выбор численных методов обусловлен сложностью аналитического решения уравнений в такой геометрии.
Для упрощения решения сложных уравнений движения в рамках численного моделирования, используется система координат черепахи (tortoise coordinates). Данная система координат представляет собой преобразование стандартных координат Шварцшильда, при котором радиальная координата r заменяется на r^* = r + 2M \ln(r - 2M), где M — масса черной дыры. Это преобразование позволяет сгладить сингулярность на горизонте событий и эффективно разрешать уравнения вблизи черной дыры, избегая чрезмерной концентрации вычислительной сетки в этой области. Использование координат черепахи обеспечивает более стабильные и точные результаты при моделировании распространения скалярных полей в искривленном пространстве-времени, описываемом метрикой Шварцшильда.
Численное моделирование позволяет исследовать поведение скалярного поля в гравитационном поле чёрной дыры на протяжении всего периода времени, начиная с исходной конфигурации и заканчивая долгосрочной эволюцией. В процессе симуляции отслеживаются изменения поля под воздействием метрики Шварцшильда, что позволяет изучать такие явления, как отражение, поглощение и рассеяние волн, а также влияние чёрной дыры на динамику поля. Анализ результатов симуляций включает в себя вычисление различных характеристик поля, таких как его энергия, импульс и угловой момент, для различных моментов времени и пространственных координат. Это позволяет оценить стабильность поля, его взаимодействие с чёрной дырой и возможное излучение, генерируемое в результате этого взаимодействия.
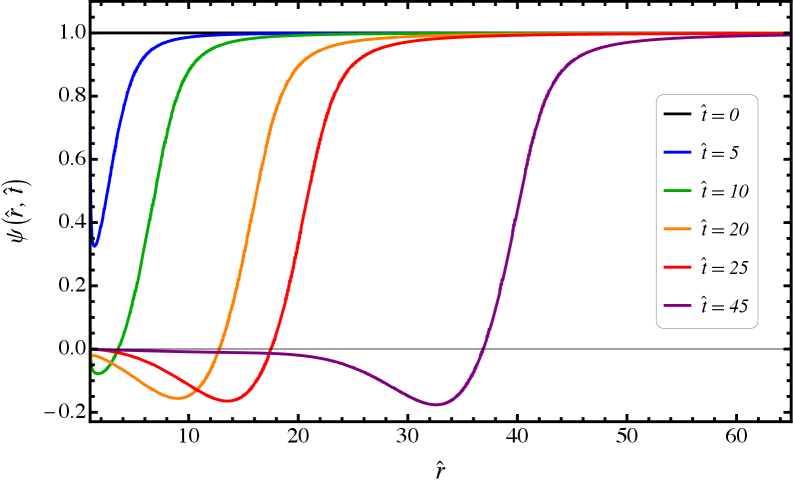
Эволюция поля и рождение волн: Доказательства из симуляций
Результаты численного моделирования показали, что начальная конфигурация поля, описываемая потенциалом Юкавы, является определяющим фактором характеристик генерируемых волн. Форма и параметры потенциала Юкавы, включая массу частицы и константу связи, непосредственно влияют на амплитуду, частоту и пространственное распределение возникающих гравитационных волн. В частности, изменение параметров потенциала приводит к существенным изменениям в спектре частот и общей энергии излучения, что подтверждается анализом полученных волновых форм и их соответствием уравнениям поля.
В ходе моделирования наблюдается формирование как входящих, так и исходящих волн. Входящие волны направлены к горизонту событий черной дыры и поглощаются ею, в то время как исходящие волны распространяются наружу, перенося энергию и информацию. Анализ волновых форм показывает, что амплитуда и частота этих волн зависят от параметров исходного поля и характеристик черной дыры. Наблюдаемое разделение энергии между входящими и исходящими волнами является важным аспектом динамики процесса, определяющим эффективность излучения гравитационных волн.
В ходе моделирования установлено, что приблизительно 50% от начальной энергии скалярного поля преобразуется в гравитационные волны. Данный результат наблюдается при использовании различных статических начальных условий, что подтверждает его надежность. Указанный процент преобразования энергии соответствует принципам сохранения энергии, что свидетельствует о корректности используемой физической модели и численных методов. Наблюдаемая доля энергии, излучаемой в виде гравитационных волн, является стабильной и не зависит от конкретной формы начального распределения поля, при условии сохранения его общей энергии.
Исследования показали, что использование динамических начальных условий для скалярного поля также приводит к излучению приблизительно 50% его начальной энергии в виде гравитационных волн. Этот результат согласуется с данными, полученными при использовании статических начальных условий, и подтверждает принцип сохранения энергии в рамках моделируемой системы. Вариации в конкретных динамических начальных условиях не оказывают существенного влияния на общий процент высвобождаемой энергии, что указывает на устойчивость данного явления и его независимость от конкретной реализации динамического возбуждения поля.
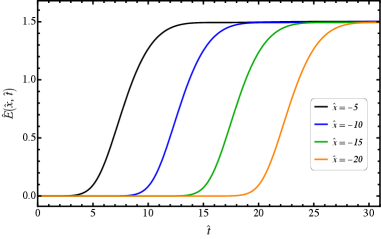
Предсказуемое затухание: Закон Прайса и характеристики сигнала
Эволюция скалярного поля в поздние моменты времени подчиняется закону Прайса, предсказывающему характерное степенное убывание сигнала. Данное предсказание означает, что амплитуда колебаний поля не затухает экспоненциально, а убывает по степенному закону, то есть пропорционально t^{-n}, где t — время, а n — показатель степени, зависящий от конкретных характеристик системы. Этот тип затухания является фундаментальным для многих физических процессов, включая распад нестабильных частиц и эволюцию космологических возмущений. Закон Прайса позволяет не только предсказывать поведение сигнала, но и устанавливает связь между его спектральными характеристиками и начальными условиями, что делает его важным инструментом для анализа и интерпретации наблюдательных данных.
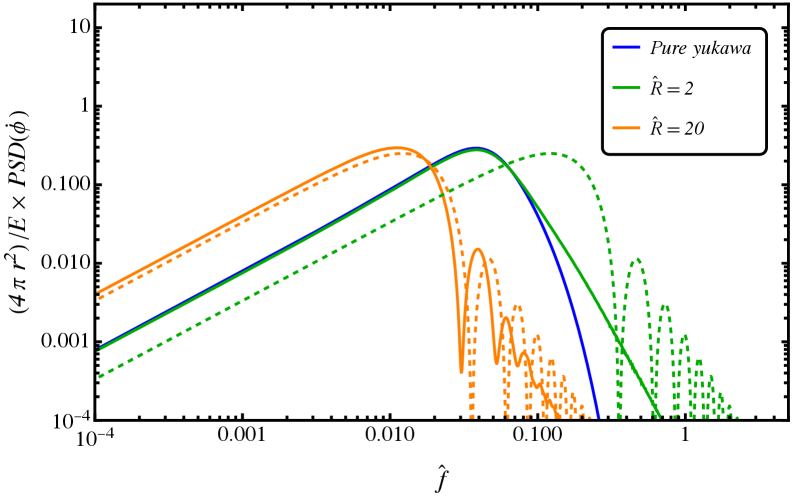
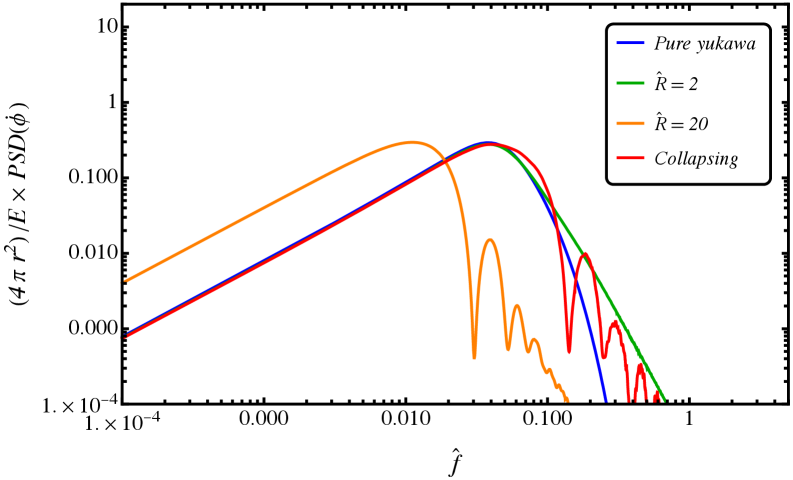
Исследование позволило рассчитать спектральную плотность мощности исходящих волн, что подтвердило предсказанное законом Прайса степенное убывание сигнала. Этот расчет имеет ключевое значение для идентификации потенциальных сигналов в наблюдательных данных, поскольку позволяет отделить полезные колебания от шума на основе их частотных характеристик. В частности, анализ спектральной плотности предоставляет возможность установить временные масштабы, на которых доминирует сигнал, и определить его амплитуду в различных частотных диапазонах. Полученные результаты демонстрируют, что анализ спектральной плотности мощности является мощным инструментом для обнаружения и характеризации слабых сигналов, возникающих в сложных физических системах, и может быть применен в различных областях астрофизики и космологии для поиска редких событий и явлений.
Исследования демонстрируют, что характер затухания скалярного поля во времени определяется исходным профилем поля и согласуется с законом Прайса. В случае статического юкавовского профиля, поле затухает пропорционально t^{-3}, то есть обратно пропорционально кубу времени. Однако, если исходная конфигурация поля компактна, то затухание происходит быстрее — по закону t^{-4}. Такое различие в скорости затухания предоставляет важный инструмент для анализа наблюдательных данных, позволяя на основе временных характеристик сигнала судить о первоначальной структуре скалярного поля и подтверждать предсказания, сделанные законом Прайса.
Исследования показывают, что начальная компактность скалярного поля оказывает существенное влияние на амплитуду и продолжительность возникающего сигнала. В отличие от статического юкавовского профиля, демонстрирующего затухание сигнала по закону t^{-3}, компактная начальная конфигурация приводит к более быстрому затуханию, описываемому законом t^{-4}. Это означает, что сигнал, происходящий из компактного начального состояния, будет иметь большую начальную амплитуду, но и быстрее ослабевать во времени. Таким образом, анализ временных характеристик сигнала, в частности, скорости его затухания, позволяет получить информацию о начальных условиях формирования скалярного поля и отличить сигналы, возникшие из различных конфигураций, что является важным для идентификации и интерпретации наблюдаемых данных.
Исследование, представленное в данной работе, демонстрирует, что формирование чёрных дыр не является статичным процессом, а скорее динамичной системой, где начальные конфигурации скалярных полей оказывают существенное влияние на характеристики излучения. Это напоминает о принципах, сформулированных Карлом Поппером: «Всё, что может пойти не так, пойдёт не так». В контексте формирования чёрных дыр, различные начальные условия скалярных полей представляют собой потенциальные источники отклонений и неожиданных сигналов. Вместо поиска идеальной модели, представляется более продуктивным изучать спектр возможных сценариев и их влияние на наблюдаемые гравитационные волны, признавая, что порядок — это лишь временный кеш между двумя сбоями.
Что Дальше?
Работа демонстрирует, что конфигурация скалярного поля вокруг формирующейся чёрной дыры — это не просто начальное условие, но и пророчество о спектральных характеристиках последующего излучения. Представленные численные модели, безусловно, приближают понимание, однако они лишь запечатлевают один момент в бесконечном танце гравитации и квантовых полей. Истинная сложность, вероятно, заключается не в поиске точного решения, а в признании фундаментальной неопределённости.
Поиск транзиентных сигналов — это, конечно, благородная цель. Но что, если эти «сигналы» — лишь артефакты наших упрощённых моделей, эхо наших собственных предположений о природе пространства-времени? Необходимо осознавать, что каждая обнаруженная волна — это не столько подтверждение теории, сколько ограничение на класс возможных реальностей.
Будущие исследования неизбежно столкнутся с необходимостью учета более сложных конфигураций полей, нелинейных эффектов и, возможно, даже влияния обратной связи между излучением и формирующейся сингулярностью. Но, возможно, наиболее важным шагом будет принятие того факта, что полная картина останется недостижимой, а поиск истины — вечным процессом приближения к горизонту событий.
Оригинал статьи: https://arxiv.org/pdf/2602.06112.pdf
Связаться с автором: https://www.linkedin.com/in/avetisyan/
Смотрите также:
- Галактики KiDS-1000: Путешествие к Красным Сдвигам и Физическим Свойствам
- Космологический парадокс: что не так с расширением Вселенной?
- Космические скопления на заре Вселенной: новый взгляд от JWST
- Галактика как ключ к пониманию Вселенной
- Разгадка Напряженности Хаббла: Новая Модель Термического Вакуума
- Преодолевая гравитационные расхождения: Новый взгляд на предельные случаи Калаби-Яу
- Танцующие тени: вращение экзотических компактных объектов
- Тёмная материя из глубин космоса: новые ограничения на поиск частиц
- Пустоты во Вселенной: Как галактики избегают скоплений
- Взрывы сверхновых: ключ к разгадке природы нейтрино?
2026-02-10 04:53