Автор: Денис Аветисян
Новое исследование показывает, как вязкость и модифицированная гравитация f(Q) могут объяснить ускоренное расширение Вселенной, снижая зависимость от сильных диссипативных эффектов.
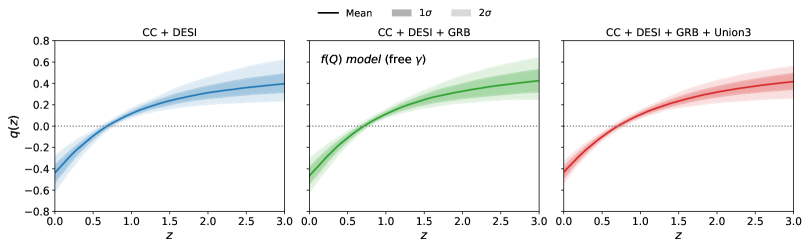
Работа посвящена исследованию космологических моделей, включающих объемную вязкость в рамках экспоненциальной гравитации f(Q), и накладывает наблюдательные ограничения на параметры этих моделей.
Космологическая модель ΛCDM, несмотря на свои успехи, требует тонкой настройки параметров и не может полностью объяснить природу тёмной энергии. В работе ‘Observational constraints on viscous free-γ fluid in $f(Q)$ gravity’ исследуются космологические последствия модифицированной теории гравитации f(Q), включающей в себя вязкую жидкость с параметром состояния γ. Полученные результаты демонстрируют, что модифицированная гравитация может эффективно объяснить наблюдаемое ускоренное расширение Вселенной, снижая потребность в сильных диссипативных эффектах. Возможно ли, что учет негеометрических свойств пространства-времени в рамках f(Q)-гравитации позволит построить более физически обоснованную и предсказательную космологическую модель?
Ускоряющаяся Вселенная и Тайна Темной Энергии
Наблюдения за далекими сверхновыми и космическим микроволновым фоном однозначно подтверждают, что расширение Вселенной не замедляется, как предсказывалось ранее, а ускоряется. Это открытие, сделанное в конце 1990-х годов, стало настоящим вызовом для стандартной космологической модели, основанной на гравитации и известной материи. Ускоряющееся расширение требует наличия некоторой формы «темной энергии», которая противодействует гравитации и заставляет пространство расширяться с нарастающей скоростью. Этот факт заставляет ученых пересматривать фундаментальные представления о природе пространства, времени и гравитации, а также искать новые физические теории, способные объяснить наблюдаемое ускорение и природу этой загадочной темной энергии. H(t) = \dot{a}(t)/a(t) — параметр Хаббла, характеризующий скорость расширения Вселенной, демонстрирует увеличение со временем, подтверждая данное ускорение.
Наблюдения за удаленными сверхновыми и космическим микроволновым фоном убедительно свидетельствуют об ускоренном расширении Вселенной. Это открытие повлекло за собой необходимость постулирования существования так называемой «темной энергии» — загадочной компоненты, составляющей приблизительно 70% от общей плотности энергии во Вселенной. Данная форма энергии, в отличие от обычной материи и темной материи, обладает отрицательным давлением, что и обуславливает ускорение расширения. Ее природа остается одной из главных загадок современной космологии, поскольку стандартные физические модели не могут адекватно объяснить ее происхождение и свойства. По сути, большая часть Вселенной состоит из чего-то, что мы практически не понимаем, и изучение темной энергии является ключевым для построения полной картины эволюции космоса.
Наиболее простое объяснение ускоренного расширения Вселенной — космологическая постоянная — сталкивается с серьезными теоретическими сложностями и проблемой тонкой настройки. В рамках квантовой теории поля предсказанный вклад вакуумной энергии в космологическую постоянную оказывается на много порядков величины больше наблюдаемой, что требует введения искусственных механизмов для подавления этого вклада. Данная несостыковка, известная как “проблема космологической постоянной”, подталкивает ученых к поиску альтернативных моделей темной энергии, таких как квинтэссенция или модифицированные теории гравитации. Эти модели предполагают, что темная энергия является динамической величиной, изменяющейся со временем, и не требует столь точной настройки параметров, как космологическая постоянная, хотя и сопряжены с собственными сложностями и требуют дальнейших исследований для подтверждения их состоятельности.
За Пределами Эйнштейна: Введение в f(Q)-Гравитацию
Гравитация f(Q) представляет собой перспективную альтернативу общей теории относительности Эйнштейна, модифицирующую ее путем замены скаляра Риччи на скаляр нонметричности, Q. В то время как общая теория относительности основана на геометрических свойствах, определяемых тензором метрики и его производными, гравитация f(Q) использует нонметричность — меру ненаправленного переноса векторов — в качестве основного геометрического объекта. Это изменение позволяет рассматривать гравитационные взаимодействия с использованием альтернативной геометрической интерпретации, потенциально избегая необходимости в постулировании темной энергии для объяснения наблюдаемого ускоренного расширения Вселенной. Формально, гравитационные уравнения в теории f(Q) выводятся из действия, зависящего от скаляра нонметричности Q и его производных, аналогично тому, как уравнения Эйнштейна выводятся из действия Гильберта-Эйнштейна.
Неметрический скаляр Q характеризует отклонение параллельного переноса векторов вдоль различных путей, что указывает на нарушение метрической связности пространства-времени. В отличие от общей теории относительности, где гравитация описывается кривизной пространства, f(Q)-гравитация использует неметричность как основной геометрический фактор, определяющий гравитационное взаимодействие. Это вводит дополнительные геометрические степени свободы, которые могут объяснить наблюдаемое ускоренное расширение Вселенной без необходимости постулировать темную энергию. Таким образом, неметричность, выраженная скаляром Q, представляет собой альтернативный механизм генерации расширения пространства, отличный от космологической постоянной или квинтэссенции.
Экспоненциальная модель f(Q), представляющая собой конкретную форму модифицированной гравитации, обеспечивает математически непротиворечивую основу для исследования эффектов, связанных с неметричностью. Данная модель предполагает функциональную зависимость гравитационного действия от скалярной неметричности Q, где f(Q) = \exp(Q). Это позволяет получить уравнения движения, свободные от сингулярностей, возникающих в стандартной космологии, и исследовать возможность объяснения ускоренного расширения Вселенной без введения темной энергии. Математическая согласованность достигается за счет соблюдения ковариантности и сохранения энергии-импульса в рамках данной теории, что позволяет проводить численные и аналитические исследования космологических моделей.
Ограничения Модели на Основе Наблюдательных Данных
Метрика Фридмана — Леметра — Робертсона — Уокера (FLRW) является основополагающим математическим инструментом для построения космологических моделей расширяющейся Вселенной. Она описывает однородную и изотропную Вселенную, предполагая, что геометрия пространства-времени может быть представлена в виде ds^2 = -dt^2 + a(t)^2 \left( \frac{dr^2}{1 - kr^2} + r^2 d\theta^2 + r^2 \sin^2\theta d\phi^2 \right), где a(t) — масштабный фактор, описывающий расширение Вселенной со временем, а k — параметр кривизны, определяющий геометрию пространства (открытое, плоское или закрытое). Использование этой метрики позволяет связать теоретические предсказания космологических моделей с наблюдаемыми данными, такими как красное смещение далеких объектов и реликтовое излучение, посредством решения уравнений Фридмана, которые следуют из общей теории относительности и описывают эволюцию масштабного фактора a(t).
Для проверки космологических моделей используются независимые измерения параметра Хаббла, получаемые с помощью различных наблюдательных методов. Сверхновые типа Ia, барионные акустические осцилляции и космические хронометры позволяют оценить текущую скорость расширения Вселенной. Полученное значение постоянной Хаббла, в диапазоне 65-68 км/с/Мпк, согласуется с результатами, полученными на основе данных миссии Planck. Это согласует наблюдаемые данные с теоретическими предсказаниями стандартной космологической модели и позволяет проводить тестирование альтернативных гравитационных теорий.
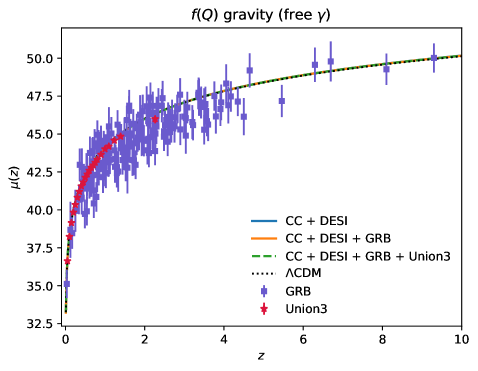
Для статистического анализа наблюдательных данных и определения параметров модели f(Q)-гравитации используются методы Марковских цепей Монте-Карло (MCMC). Оценка качества соответствия модели проводится путем сравнения с ΛCDM-моделью. При анализе данных сверхновых типа Ia из каталога Union3 для свободно-вязкой модели с параметром γ, наблюдается значение Δχ² = -8.9, что указывает на сопоставимое качество соответствия с ΛCDM-моделью. Это означает, что модель f(Q)-гравитации, с учетом данных о сверхновых, может адекватно описывать наблюдаемую расширяющуюся Вселенную, не уступая в точности стандартной ΛCDM-модели.
Уточнение Картинки: Диагностика и Перспективы Будущих Исследований
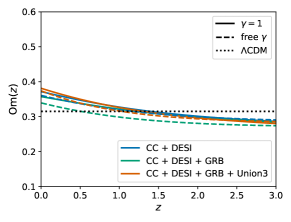
Геометрические методы диагностики, такие как Statefinder Diagnostics и Om(z) Diagnostic, представляют собой эффективный инструмент для характеристики и разграничения различных космологических моделей, включая альтернативные теории гравитации, например, f(Q)-гравитацию. Эти диагностические инструменты позволяют построить графики, отображающие эволюцию Вселенной во времени и пространстве, что позволяет отличить модели, предсказывающие различную динамику расширения. В частности, анализ этих графиков позволяет оценить отклонение от стандартной \Lambda CDM модели и определить, какие параметры наиболее чувствительны к изменениям в базовой физике. Применение данных методов к f(Q)-гравитации демонстрирует, что данная модель способна обеспечить ускоренное расширение Вселенной, при этом предлагая альтернативное объяснение темной энергии и расширяя наше понимание фундаментальных законов, управляющих космосом.
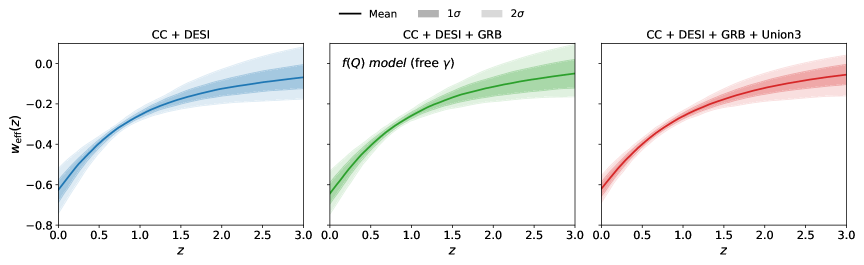
Учёт вязкости объёма в уравнении состояния позволяет получить более полную физическую картину расширения Вселенной. Исследования показывают, что модель f(Q)-гравитации достигает сопоставимого ускорения при значительно меньшем коэффициенте вязкости объёма ζ, составляющем 0.3-0.5. Это существенно ниже, чем в случае гравитационной модели Эйнштейна (GR) с учётом вязкости, где наблюдаются значения в диапазоне 1.6-2.2. Такое различие указывает на потенциальную способность f(Q)-гравитации более эффективно объяснять наблюдаемое ускорение Вселенной без необходимости прибегать к столь значительной вязкости, что делает её перспективным направлением для дальнейших исследований в области тёмной энергии и космологии.
Постоянное совершенствование наблюдательных данных и теоретических моделей открывает перспективы для раскрытия истинной природы тёмной энергии и фундаментальных законов, управляющих расширением Вселенной. Улучшение точности измерений космологических параметров, таких как постоянная Хаббла и плотность тёмной энергии, в сочетании с разработкой более сложных теоретических рамок, выходящих за рамки стандартной \Lambda CDM модели, позволит проверить альтернативные теории гравитации и более точно определить уравнение состояния тёмной энергии. Особое внимание уделяется исследованиям, направленным на уменьшение систематических ошибок в наблюдениях за сверхновыми типа Ia, барионными акустическими колебаниями и космическим микроволновым фоном. Сочетание этих усилий может привести к революционным открытиям, пролившим свет на фундаментальные аспекты космологии и эволюции Вселенной.
Исследование, представленное в статье, демонстрирует, как модифицированная гравитация в рамках f(Q) теории способна объяснить ускоренное расширение Вселенной с меньшей зависимостью от сильных диссипативных эффектов. Это подчеркивает адаптивность систем, их способность к эволюции и приспособлению к изменяющимся условиям. В этой связи вспоминается высказывание Блеза Паскаля: «Все великие дела требуют времени». Действительно, подобно тому, как космологические модели нуждаются в тщательной проверке и уточнении, системы тоже нуждаются во времени для проявления своей зрелости и эффективности. Работа демонстрирует, что введение вязкости в космологические модели, хотя и требует тонкой настройки параметров, может стать ключевым шагом к более полному пониманию динамики Вселенной и ее долгосрочной эволюции.
Что впереди?
Представленная работа, подобно любой хронике, фиксирует лишь мгновение в нескончаемом течении космологических исследований. Попытка описать ускорение Вселенной посредством модифицированной гравитации f(Q) и вязкости — это не столько решение, сколько уточнение вопросов. Неизвестно, является ли вязкость фундаментальным свойством космоса или лишь артефактом неполного понимания. Логирование процессов в этой области неизбежно выявляет новые, более тонкие детали, требующие объяснения.
Очевидно, что дальнейшее исследование требует не только более точных космологических данных, но и углубленного анализа математической структуры f(Q) гравитации. Вопрос о стабильности решений и их связи с наблюдаемой физикой остается открытым. Подобно любой системе, f(Q) гравитация подвержена старению — ее адекватность будет определяться способностью адаптироваться к новым данным и теоретическим вызовам.
Развертывание новых моделей требует осторожности. Стремление к элегантности и простоте должно быть уравновешено необходимостью объяснения наблюдаемых явлений. В конечном счете, цель состоит не в том, чтобы создать наиболее сложное описание Вселенной, а в том, чтобы найти наиболее достойный способ ее понимания, даже если этот процесс окажется бесконечным.
Оригинал статьи: https://arxiv.org/pdf/2602.16757.pdf
Связаться с автором: https://www.linkedin.com/in/avetisyan/
Смотрите также:
- За гранью сохранения барионного числа: поиск новой физики
- Вселенная в фокусе: Новый взгляд на постоянную Хаббла
- Космический Гистерезис: Отскок Вселенной и Роль Тorsion
- Тайны Ранней Вселенной и Скрытые Нейтрино
- Гравитация под вопросом: Проверка моделей модифицированной гравитации
- Поиск темной энергии: новый алгоритм для точного измерения расширения Вселенной
- Тёмная материя под прицетом гравитационных линз
- Вселенная в цифрах: современный взгляд на космологические параметры
- Сингулярности аномальных размерностей: новый взгляд на структуру операторов
- Искривление пространства: Разбираемся в теории варп-двигателей
2026-02-20 23:57