Автор: Денис Аветисян
Новое исследование анализирует квазипериодические колебания в аккреционных дисках вокруг вращающихся черных дыр, позволяя уточнить параметры моделей и проверить предсказания общей теории относительности.
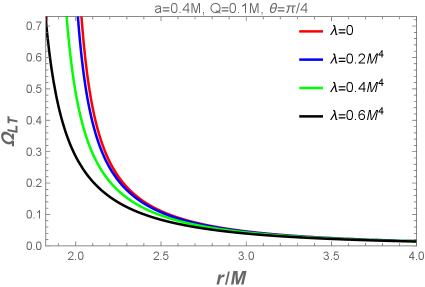
Анализ прецессии и квазипериодических колебаний позволяет установить ограничения на параметры вращающихся заряженных черных дыр и подтвердить соответствие общей теории относительности.
Несмотря на успехи общей теории относительности, многие вопросы, связанные с физикой черных дыр, остаются открытыми. В работе «Precessions and parameter constraints from quasiperiodic oscillations in a rotating charged black hole» исследуется возможность использования квазипериодических осцилляций (QPO) из рентгеновских двойных систем для изучения эффектов увлечения пространства-времени и физики аккреционных дисков вокруг вращающихся регулярных магнитных черных дыр. Показано, что анализ прецессии связанных орбит и эпициклических осцилляций позволяет наложить ограничения на параметры черной дыры, включая массу, спин, магнитный заряд и параметр неминимального взаимодействия, подтверждая соответствие результатов предсказаниям общей теории относительности. Какие новые ограничения на свойства черных дыр можно будет получить при более детальном анализе данных о QPO и прецессиях в будущем?
В поисках гармонии: Пределы метрики Керра
Метрика Керра, являющаяся краеугольным камнем современных представлений о вращающихся чёрных дырах, несмотря на свою успешность, может не в полной мере отражать всю сложность этих объектов, особенно в отношении магнитных полей. Дело в том, что стандартная метрика Керра предполагает идеализированную ситуацию, игнорируя наличие и влияние магнитных полей, которые, как показывают наблюдения и теоретические модели, неизбежно присутствуют вокруг чёрных дыр. Эти поля возникают из аккреционного диска, состоящего из ионизированной материи, вращающейся вокруг чёрной дыры, и оказывают значительное влияние на динамику окружающего пространства-времени, изменяя геометрию вокруг объекта и даже влияя на испускаемое излучение. Игнорирование магнитных полей может приводить к неточностям в предсказаниях относительно наблюдаемых явлений, таких как квазипериодические осцилляции QPO и эффекты прецессии, что подчеркивает необходимость разработки более совершенных моделей, учитывающих взаимодействие гравитации и электромагнетизма вблизи чёрных дыр.
Существующие модели вращающихся черных дыр, основанные на метрике Керра, сталкиваются с трудностями при точном предсказании наблюдаемых астрономических явлений, таких как квазипериодические колебания (QPO) и эффекты прецессии аккреционного диска. Эти колебания, проявляющиеся в изменениях интенсивности излучения, и прецессия оси вращения диска вокруг черной дыры, не могут быть полностью объяснены в рамках упрощенных математических моделей. Несоответствие между теоретическими предсказаниями и наблюдениями указывает на необходимость учета дополнительных физических факторов, таких как сложные магнитные поля, турбулентность в аккреционном диске, и релятивистские эффекты, которые оказывают влияние на динамику вещества вблизи черной дыры. Более точное моделирование этих явлений является ключевым для проверки общей теории относительности в экстремальных гравитационных условиях и углубления понимания физики черных дыр.
Изучение тонкостей динамики вращающихся черных дыр имеет первостепенное значение для проверки общей теории относительности в экстремальных гравитационных режимах. Наблюдения за аккреционными дисками вокруг черных дыр, в особенности анализ квазипериодических осцилляций (QPO) и эффектов прецессии, предоставляют уникальную возможность для сопоставления теоретических предсказаний с реальностью. Отклонения от предсказаний, основанных на метрике Керра, могут указывать на необходимость пересмотра фундаментальных представлений о гравитации и природе черных дыр. Более того, детальный анализ этих явлений позволяет исследовать области, где общая теория относительности может требовать модификаций или дополнений, открывая путь к разработке более полной и точной теории гравитации, способной объяснить все наблюдаемые вселенные феномены.
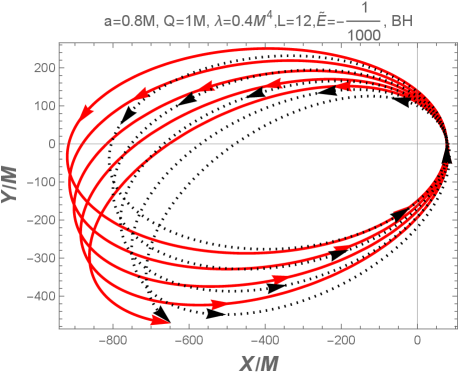
Новая геометрия: Вращающиеся регулярные магнитные чёрные дыры
В рамках настоящего исследования рассматривается геометрия пространства-времени, описывающая вращающуюся регулярную магнитную черную дыру, как потенциальное уточнение решения Керра. Данная модель предполагает наличие магнитного заряда и параметра неминимального связывания, что позволяет более детально описать свойства черных дыр и исследовать отклонения от классического решения Керра. Анализ проводится в рамках общей теории относительности, с целью определения условий, при которых данная геометрия может представлять физически реалистичную модель астрофизических черных дыр и прогнозировать отличия в наблюдаемых эффектах, таких как гравитационное линзирование или излучение Хокинга, по сравнению с предсказаниями, основанными на метрике Керра. g_{\mu\nu} тензор метрики, описывающий данную геометрию, отличается от метрики Керра наличием дополнительных членов, зависящих от магнитного заряда и параметра неминимального связывания.
Данная модель включает в себя магнитный заряд и параметр неминимальной связи, что позволяет получить более детальное описание свойств чёрных дыр. Введение магнитного заряда P в геометрию чёрной дыры позволяет исследовать влияние электромагнитных полей на структуру пространства-времени вокруг объекта. Параметр неминимальной связи β описывает отклонение от стандартного взаимодействия между гравитацией и электромагнетизмом, предусмотренного классической теорией, и позволяет модифицировать метрику пространства-времени, что влияет на такие характеристики, как горизонт событий и эргосфера. Изменение этих параметров позволяет исследовать более широкий спектр решений, чем в случае классической метрики Керра, и потенциально описывать чёрные дыры со сложными электромагнитными полями.
Данное исследование вращающихся регулярных магнитных чёрных дыр базируется на устоявшемся теоретическом фундаменте — Общей теории относительности (ОТО) Эйнштейна. В рамках ОТО гравитация описывается как геометрическое свойство пространства-времени, искривляемого массой и энергией. Уравнения Эйнштейна, G_{\mu\nu} = 8\pi T_{\mu\nu}, являются ключевым инструментом для анализа гравитационных полей и построения моделей чёрных дыр. Используя метрику пространства-времени, удовлетворяющую этим уравнениям, мы исследуем свойства вращающихся чёрных дыр с учётом электромагнитного поля и параметров, выходящих за рамки классического решения Керра.
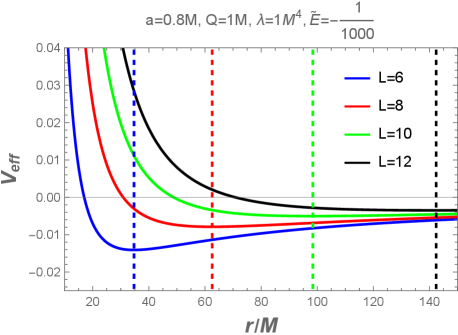
Наблюдаемые сигнатуры: Прецессия и увлечение пространства-времени
Вращающиеся регулярные магнитные чёрные дыры предсказывают характерные эффекты прецессии, включая прецессию периастра и прецессию узла, обусловленные искажением геометрии пространства-времени. Прецессия периастра проявляется в изменении ориентации эллиптической орбиты объекта вокруг черной дыры, в то время как прецессия узла касается вращения плоскости орбиты. Величина этих эффектов напрямую зависит от спина черной дыры и параметров орбиты, таких как эксцентриситет и большая полуось. Наблюдение этих прецессионных эффектов может служить прямым доказательством существования вращающихся черных дыр и позволит определить их угловой момент.
Эффект увлечения инерциальных систем отсчета, известный как увлечение пространства-времени или Frame-Dragging, является прямым следствием вращения массивных объектов, таких как вращающиеся черные дыры. Этот эффект проявляется в том, что вращение объекта искривляет окружающее пространство-время, заставляя орбиты близлежащих объектов прецессировать и отклоняться от ньютоновской геометрии. Влияние наиболее заметно вблизи вращающегося объекта, где скорость вращения и гравитационное поле максимальны. Величина увлечения пропорциональна угловой скорости вращения объекта и его массе, определяя степень искажения пространства-времени и, следовательно, отклонение орбит близлежащих тел.
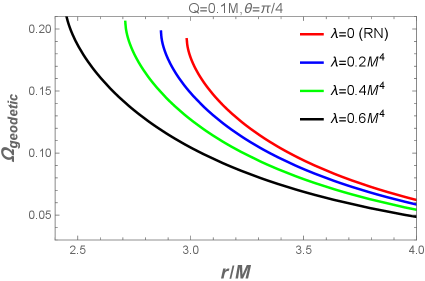
Прецессия спина проявляется как результат совместного влияния эффектов, связанных с вращением чёрной дыры, и включает в себя два основных компонента. Геодезическая прецессия возникает из-за искривления пространства-времени, вызванного массой вращающейся чёрной дыры, и влияет на ориентацию плоскости орбиты. Прецессия Лензе-Тирринга, также известная как увлечение инерциальных систем отсчёта, возникает из-за вращения самого пространства-времени вокруг чёрной дыры и приводит к медленному изменению ориентации оси вращения объекта на орбите. Оба этих эффекта, \omega_{Geodesic} и \omega_{Lense-Thirring}, суммируются, определяя общую прецессию спина вращающихся объектов вблизи чёрной дыры.
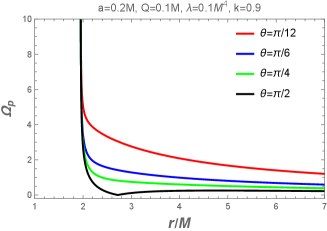
Ограничение модели с помощью QPO и MCMC
Рентгеновские двойные системы являются идеальной наблюдательной платформой для изучения динамики черных дыр благодаря испускаемым ими квазипериодическим колебаниям (QPO). Эти колебания представляют собой небольшие, временные изменения в рентгеновском излучении, генерируемом аккреционным диском вокруг черной дыры. Анализ QPO позволяет извлекать информацию о параметрах черной дыры, таких как ее масса и спин, поскольку частоты и амплитуды колебаний чувствительны к геометрии и динамике аккреционного диска, а также к гравитационному полю черной дыры. Изучение QPO предоставляет уникальную возможность проверить предсказания теоретических моделей и углубить наше понимание физики черных дыр и аккреции.
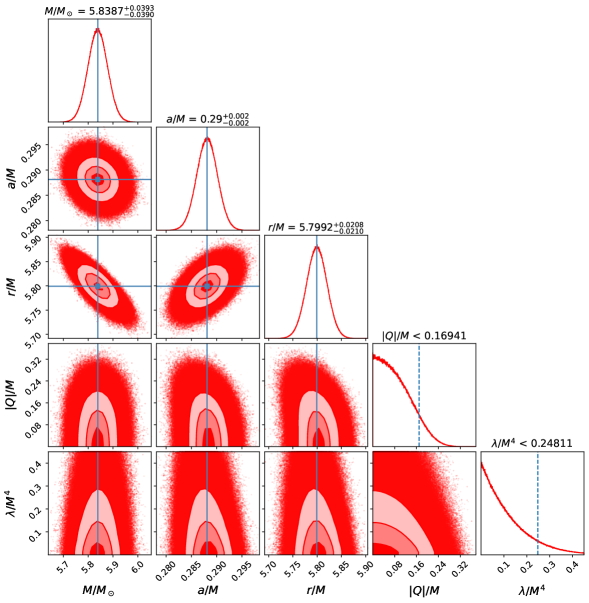
Анализ квазипериодических осцилляций (QPO) используется для извлечения информации о параметрах чёрной дыры, основываясь на уникальных сигнатурах, предсказанных теоретической моделью. QPO проявляются как модуляции в рентгеновском излучении, и их частота и амплитуда зависят от характеристик аккреционного диска и вращения чёрной дыры. Используя спектральный анализ и моделирование динамики аккреционного диска, мы можем связать наблюдаемые характеристики QPO с параметрами, такими как скорость вращения чёрной дыры и внутренний радиус диска. Этот подход позволяет оценить такие параметры, как Q/M и \lambda/M^4, определяющие деформацию пространства-времени вокруг чёрной дыры.
Для точного определения границ параметров модели использовалось моделирование методом Монте-Карло Маркова (MCMC). В результате анализа, установлено, что абсолютное значение отношения |Q/M| не превышает 0.16941, а отношение \lambda/M^{4} — 0.24, при уровне достоверности 90%. Полученные ограничения позволяют сузить область возможных значений параметров и более точно характеризовать динамику аккреционного диска вокруг черной дыры в рентгеновской двойной системе.
Влияние на наше понимание пространства-времени и перспективы будущих исследований
Исследования показали, что вращающиеся регулярные магнитные чёрные дыры обладают значительным потенциалом для углубления понимания физики чёрных дыр. В отличие от классических решений, описывающих сингулярности, данная модель предполагает наличие регулярного ядра, что позволяет избежать проблем, связанных с бесконечностями в центре чёрной дыры. Это открывает возможности для изучения физических процессов вблизи горизонта событий более реалистичным образом, а также для объяснения наблюдаемых астрономических явлений, таких как аккреционные диски и джеты, без привлечения экзотических форм материи. Полученные результаты указывают на то, что вращающиеся регулярные магнитные чёрные дыры могут служить более полной и адекватной моделью для описания этих загадочных объектов во Вселенной, предоставляя новые инструменты для изучения гравитации и космологии.
Разработанная структура ZAMO (Zero Angular Momentum Observer) представляет собой ценный инструмент для анализа прецессии орбит вблизи вращающихся черных дыр. Она позволяет исследователям интерпретировать тонкие изменения в траекториях движения объектов, вызванные искривлением пространства-времени, и извлекать важную информацию о геометрии окружающего пространства. В отличие от традиционных методов, ZAMO фокусируется на наблюдателях, находящихся в нулевом угловом моменте относительно черной дыры, что позволяет более точно моделировать гравитационные эффекты и отделять их от других факторов, влияющих на прецессию. Использование ZAMO открывает возможности для более глубокого понимания структуры пространства-времени вблизи экстремальных гравитационных объектов и проверки предсказаний общей теории относительности в сильных гравитационных полях.
Дальнейшие исследования будут направлены на усовершенствование разработанной модели вращающихся регулярных магнитных чёрных дыр. Предстоит включить в неё дополнительные физические эффекты, такие как влияние аккреционного диска и спина частиц, для повышения реалистичности и точности предсказаний. Особое внимание будет уделено проверке теоретических результатов с помощью высокоточных астрономических наблюдений, в частности, анализа прецессии орбит звёзд вблизи чёрных дыр и гравитационных волн, регистрируемых современными детекторами. Такой подход позволит не только подтвердить или опровергнуть предложенную модель, но и глубже понять фундаментальные свойства пространства-времени и природу чёрных дыр, открывая новые горизонты в астрофизике и гравитационной физике.
Исследование квазипериодических осцилляций (QPO) вокруг вращающихся регулярных магнитных черных дыр, представленное в работе, подобно попытке прочесть послание, закодированное в самом времени. Каждое смещение параметров, каждая выявленная прецессия спина, является эхом, отражающимся от гравитационных горизонтов. Как отметил Бертран Рассел: «Страх — это признак того, что мы живем слишком много в будущем». В контексте данной работы, точность определения параметров вращения черной дыры — это попытка зафиксировать настоящее, понять текущее состояние системы, прежде чем оно растворится в неопределенности будущего. Анализ QPO и прецессии спина позволяет не только подтвердить соответствие общей теории относительности, но и глубже понять динамику этих экзотических объектов, их взаимодействие со временем и пространством.
Куда же дальше?
Каждый коммит в летописи исследований вращающихся чёрных дыр — это попытка зафиксировать момент истины, но и признание её неуловимости. Данная работа, анализируя квазипериодические колебания и прецессию спина, лишь подтверждает, что кажущаяся простота уравнений общей теории относительности скрывает сложность реальных систем. Ограничения, накладываемые на параметры регулярных чёрных дыр, — это не столько окончательные ответы, сколько указатели на новые вопросы. Что, если отклонения от общей теории относительности не случайны, а отражают фундаментальные свойства пространства-времени, которые пока не поддаются описанию?
Задержка исправлений — это налог на амбиции, и в данном случае — на стремление создать модель, охватывающую всё многообразие наблюдаемых явлений. Следующим шагом видится не столько повышение точности расчётов, сколько разработка новых наблюдательных стратегий, способных уловить тонкие эффекты, предсказываемые различными теориями. Необходимо выйти за рамки анализа квазипериодических колебаний и изучить другие проявления гравитационных волн, которые могут содержать ключи к пониманию природы чёрных дыр.
Время — не метрика, а среда, в которой существуют системы. И в этой среде, каждый новый результат — это лишь новая точка отсчёта, напоминающая о том, что познание — это бесконечный процесс, а не достижение конечной цели. Поиск ответов на вопросы о природе чёрных дыр — это не столько решение конкретной научной задачи, сколько философское упражнение, заставляющее задуматься о пределах познания и месте человека во Вселенной.
Оригинал статьи: https://arxiv.org/pdf/2602.11525.pdf
Связаться с автором: https://www.linkedin.com/in/avetisyan/
Смотрите также:
- Галактика как ключ к пониманию Вселенной
- Тёмная энергия: новые сигналы из глубин Вселенной
- За гранью Стандартной модели: новые ограничения на взаимодействия нейтрино
- Карты неба: Новый взгляд на крупномасштабную структуру Вселенной
- Космологический парадокс: что не так с расширением Вселенной?
- Разгадка Напряженности Хаббла: Новая Модель Термического Вакуума
- Радиоэхо столкновений: активные ядра галактик в слиящихся группах
- Космические нити рождения звёзд: обнаружены структуры в плотных облаках
- Вселенная в фокусе: Новый взгляд на постоянную Хаббла
- Танцующие тени: вращение экзотических компактных объектов
2026-02-14 06:28