Танцы гигантов: Как космологическая постоянная влияет на спиральные бинарные системы

Автор: Денис Аветисян

Новое исследование раскрывает влияние расширяющейся Вселенной на поведение экстремальных бинарных систем, предсказывая изменения в их орбитальной эволюции и гравитационных волнах.

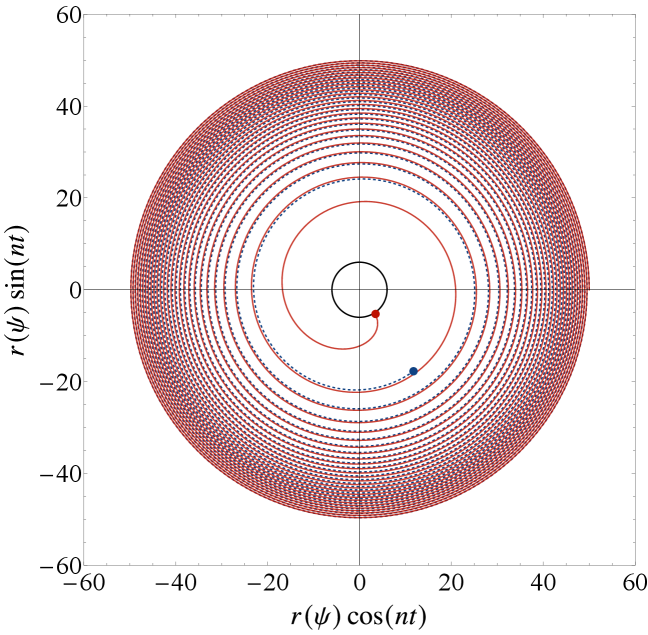
На пространстве-времени с <span class="katex-eq" data-katex-display="false">\lambda = 10^{-7}</span>, траектории круговых орбит в метрике Шварцшильда и Шварцшильда-де Ситтера демонстрируют пренебрежимо малые отклонения на коротких временных масштабах, однако при увеличении времени космологическая постоянная в метрике де Ситтера ускоряет эволюцию орбит, приводя к более быстрому достижению сепаратрисы или, наоборот, к более раннему погружению в чёрную дыру. — На пространстве-времени с $\lambda = 10^{-7}$ , траектории круговых орбит в метрике Шварцшильда и Шварцшильда-де Ситтера демонстрируют пренебрежимо малые отклонения на коротких временных масштабах, однако при увеличении времени космологическая постоянная в метрике де Ситтера ускоряет эволюцию орбит, приводя к более быстрому достижению сепаратрисы или, наоборот, к более раннему погружению в чёрную дыру.

Работа посвящена анализу орбитальной динамики систем с экстремальным соотношением масс в пространстве Шварцшильда — де Ситтера с учетом космологической постоянной.

В стандартных моделях гравитационного излучения, как правило, пренебрегают влиянием космологической постоянной на динамику компактных бинарных систем. В статье ‘Extreme-mass ratio inspirals in Schwarzschild — de Sitter spacetime I: Weak-field orbits’ исследуется влияние космологической постоянной на орбитальную эволюцию систем с экстремальным соотношением масс, в частности, на стадии медленного сближения объектов. Показано, что даже небольшое положительное значение космологической постоянной ускоряет уменьшение эксцентриситета орбиты, сокращая время до погружения и, следовательно, влияя на оценки частоты событий для будущих космических детекторов. Как именно космологическая постоянная может изменить наши представления о гравитационных волнах от слияния черных дыр и нейтронных звезд, и какие новые возможности для исследования расширяющейся Вселенной это открывает?

Танцы в Искривлённом Пространстве: Основы Двойной Эволюции

Понимание динамики объектов в искривлённом пространстве-времени, описываемом метрикой Шварцшильда-де Ситтера, является основополагающим для точного моделирования эволюции двойных звёздных систем. Данная метрика учитывает как гравитационное воздействие массы, так и влияние космологической постоянной, определяющей ускоренное расширение Вселенной. Именно искривление пространства-времени, а не просто гравитационная сила в классическом понимании, определяет траектории движения тел в системе. $g_{\mu\nu}$ тензор метрики описывает геометрию пространства-времени, определяя, как измеряются расстояния и время для наблюдателя, что критически важно для расчета орбит и предсказания долгосрочной эволюции двойных систем, включая процессы спирализации и слияния.

Траектории массивных частиц в искривлённом пространстве-времени, определяемые так называемыми времениподобными геодезическими, полностью определяют орбитальное поведение двойных звёздных систем. Эти геодезические — кратчайшие пути между двумя точками в искривлённом пространстве — не являются простыми эллипсами, как в ньютоновской механике. Вместо этого, их форма подвержена влиянию гравитационного поля и космологической постоянной, что приводит к прецессии периастриона и другим релятивистским эффектам. Изучение этих геодезических позволяет точно моделировать эволюцию двойных систем, предсказывая изменения в их орбитальных параметрах с течением времени и, что особенно важно, оценивать скорость потери энергии и углового момента посредством гравитационного излучения. Понимание принципов движения по времениподобным геодезическим является фундаментальным для интерпретации наблюдаемых сигналов от гравитационных волн, испускаемых сливающимися чёрными дырами и нейтронными звёздами.

Точное вычисление потерь энергии и углового момента посредством гравитационного излучения является ключевым для моделирования эволюции двойных систем. Исследования показывают, что космологическая постоянная оказывает заметное влияние на данный процесс, модифицируя скорость спирализации объектов. В частности, присутствие космологической постоянной приводит к изменению амплитуды и частоты гравитационных волн, испускаемых при сближении масс. Это, в свою очередь, влияет на время, необходимое для слияния компонентов двойной системы, а также на характеристики детектируемого сигнала. $\Delta t \propto \frac{1}{\Lambda}$ , где Λ — космологическая постоянная, демонстрирует обратную зависимость между скоростью спирализации и величиной космологической постоянной. Таким образом, анализ гравитационного излучения позволяет не только изучать эволюцию двойных систем, но и проводить независимые проверки космологической модели Вселенной.

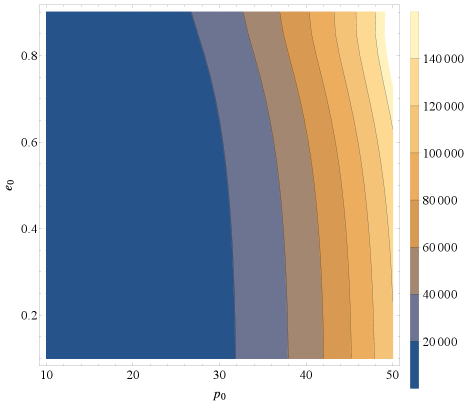
Численное моделирование времени погружения показывает, что учет самосогласованной эволюции параметров (p, e) уменьшает это время для пространства-времени Шварцшильда и SdS, при этом увеличение рассматриваемого временного масштаба расширяет область начальных параметров и потенциальных источников гравитационных волн, а также указывает на более медленное затухание орбит с высокой эксцентриситетом.

Укрощение Сложности: Аналитические Инструменты для Двойных Систем

Адиабатическое приближение значительно упрощает анализ эволюции орбит, основываясь на предположении о медленном изменении параметров системы по сравнению с периодом обращения. В рамках этого приближения, изменение параметров орбиты, таких как большая полуось или эксцентриситет, рассматривается как квази-статический процесс. Это позволяет пренебречь быстрыми колебаниями и рассматривать орбиту как последовательность равновесных состояний, изменяющихся со временем. Математически, это выражается в сохранении некоторых интегралов движения в процессе эволюции, что существенно снижает сложность решаемых уравнений и позволяет получить аналитические решения в случаях, когда точное решение невозможно. Данный метод особенно эффективен при исследовании орбит, подверженных медленным возмущениям, например, вызванным гравитационным излучением или внешними силами.

Пост-ньютоновское приближение, в сочетании с адиабатическим приближением, представляет собой пертурбативный метод решения уравнений Эйнштейна в области слабых гравитационных полей. Этот подход позволяет разложить решение уравнений в ряд по малой параметру — отношению скорости объектов к скорости света $v/c$ . В рамках данного метода, метрика пространства-времени записывается как сумма метрики Минковского и возмущений, пропорциональных $v^2/c^2$ , $v^4/c^4$ и так далее. Пост-ньютоновские вычисления используются для анализа движения тел в слабых гравитационных полях, например, в задачах небесной механики и для расчета гравитационного излучения, генерируемого двойными системами.

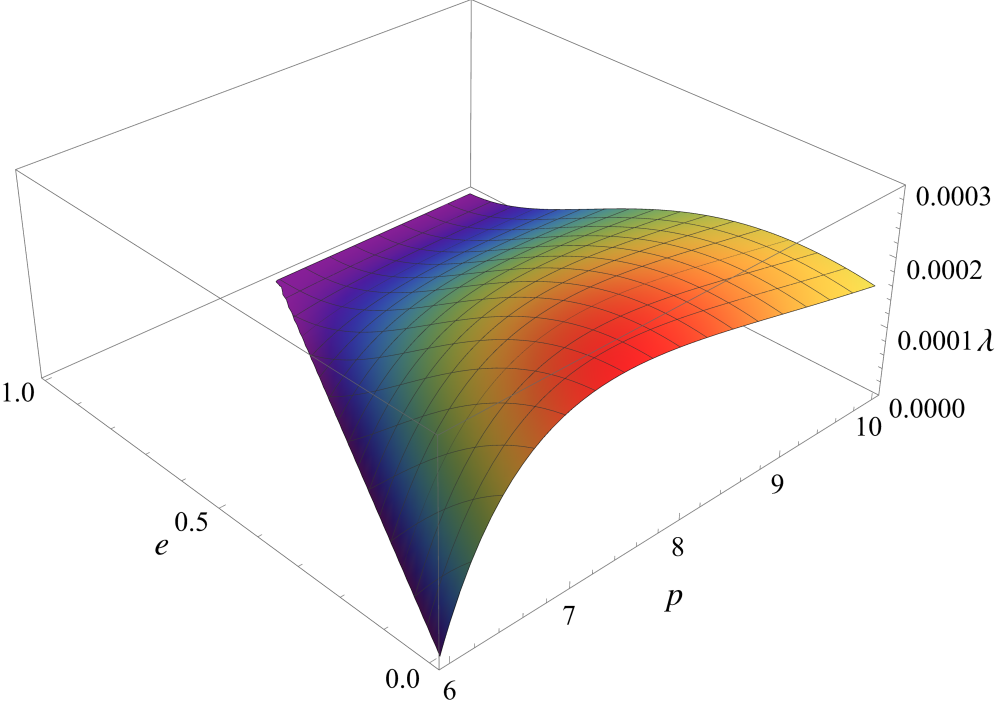
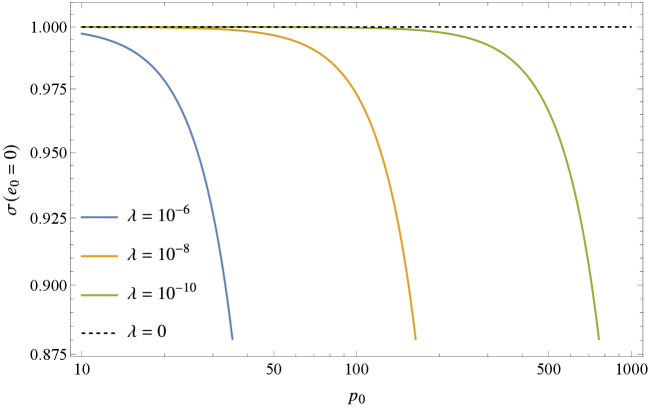
Используя адиабатическое и пост-ньютоновское приближения, возможно вычисление ключевых параметров, влияющих на траекторию двойной системы и характеристики генерируемых гравитационных волн. В частности, введение космологической постоянной в расчеты приводит к специфической зависимости эксцентриситета орбиты от времени, отличной от результатов, получаемых в рамках стандартных пост-ньютоновских вычислений. Эта зависимость проявляется в модификации фазового сдвига гравитационных волн и оказывает влияние на точность определения параметров системы по сигналам, регистрируемым гравитационно-волновыми детекторами. Влияние космологической постоянной наиболее заметно на поздних стадиях эволюции двойной системы, когда скорость сближения компонентов становится относительно небольшой.

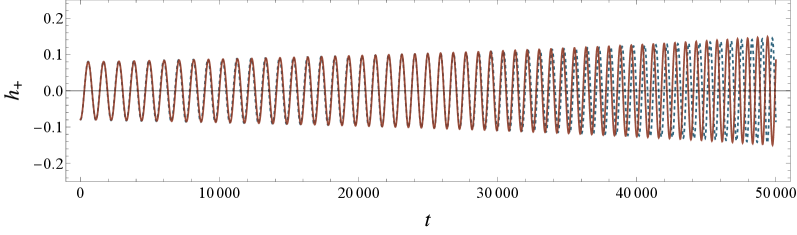
Сравнение адиабатических волновых форм для метрики Шварцшильда <span class="katex-eq" data-katex-display="false">\lambda = 0</span> (синяя линия) и пространства SdS с <span class="katex-eq" data-katex-display="false">\lambda = 10^{-7}</span> (красная линия) показывает, что космологическая постоянная увеличивает амплитуду и вызывает начальную задержку фазы волны для обеих поляризаций (плюс и крест) при начальной эксцентриситете <span class="katex-eq" data-katex-display="false">e_0 = 0.7</span> и для круговой орбиты. — Сравнение адиабатических волновых форм для метрики Шварцшильда $\lambda = 0$ (синяя линия) и пространства SdS с $\lambda = 10^{-7}$ (красная линия) показывает, что космологическая постоянная увеличивает амплитуду и вызывает начальную задержку фазы волны для обеих поляризаций (плюс и крест) при начальной эксцентриситете $e_0 = 0.7$ и для круговой орбиты.

Границы Стабильности: Судьба Компактных Объектов в Двойных Системах

Сепаратриса представляет собой критическую границу в пространстве параметров, разделяющую траектории компактных объектов на два основных типа: спиральные (Plunging Orbit), ведущие непосредственно к поглощению черной дырой, и рассеивающие (Scattering Orbit), при которых объект отклоняется и покидает систему. Различие между этими траекториями определяется начальными условиями, такими как энергия и угловой момент объекта, относительно гравитационного поля центрального тела. Пересечение сепаратрисы означает качественное изменение динамики, определяя, произойдет ли захват объекта черной дырой или он будет рассеян обратно в пространство. Таким образом, точное определение положения сепаратрисы является ключевым для прогнозирования конечной судьбы компактных объектов в бинарных системах.

Положение сепаратрисы, критической границы, разделяющей траектории компактных объектов, напрямую зависит от геометрии окружающего пространства-времени и характеристик двойной системы. В частности, положение сепаратрисы определяется параметрами, заданными уравнениями $(2.3.1)$ и $(2.30)$ , которые учитывают массы компонентов системы, их угловой момент и другие ключевые величины, определяющие гравитационное взаимодействие. Изменение этих параметров приводит к соответствующему смещению сепаратрисы, что влияет на вероятность спирального погружения объекта в черную дыру или его отклонения и выхода из системы.

Точное картирование границы сепаратрисы критически важно для прогнозирования конечной судьбы компактных объектов в двойных системах и характеристик генерируемых ими гравитационных волн. Определение положения этой границы позволяет установить модификации внутренних и внешних границ стабильных орбит, влияющие на траектории движения объектов и, следовательно, на наблюдаемые сигналы. Изменение положения сепаратрисы, определяемое параметрами системы, напрямую коррелирует с вероятностью спирального падения объекта в черную дыру или его рассеяния, что влияет на амплитуду и частоту испускаемых гравитационных волн и позволяет проводить более точные измерения параметров системы, включая массы и спины компонентов.

Уравнение сепаратрисы <span class="katex-eq" data-katex-display="false">P(p,e,\lambda)</span> определяет допустимую область параметров для устойчивых связанных орбит на фазовой плоскости <span class="katex-eq" data-katex-display="false">(p,e)</span>, при этом увеличение космологической постоянной λ может привести к распаду даже орбит с большим разделением. — Уравнение сепаратрисы $P(p,e,\lambda)$ определяет допустимую область параметров для устойчивых связанных орбит на фазовой плоскости $(p,e)$ , при этом увеличение космологической постоянной λ может привести к распаду даже орбит с большим разделением.

Экстремальные Спирали и Обнаружение Гравитационных Волн: От Теории к Наблюдениям

Экстремальные спирали массивных объектов — это процессы, в которых компактный объект, сравнимый по массе со звездой, постепенно приближается к сверхмассивной чёрной дыре и в конечном итоге поглощается ею. Данное взаимодействие порождает уникальные гравитационные волны, отличающиеся от тех, что возникают при слиянии двух чёрных дыр сопоставимой массы. Эти волны характеризуются длительным, постепенно усиливающимся сигналом, поскольку объект спирально приближается к горизонту событий. Специфика формы сигнала обусловлена значительной разницей в массах взаимодействующих объектов, что приводит к появлению характерных частотных и амплитудных изменений, позволяющих идентифицировать и изучать эти редкие события во Вселенной. Изучение этих гравитационных волн предоставляет уникальную возможность проверить общую теорию относительности в экстремальных гравитационных условиях и получить информацию о свойствах сверхмассивных чёрных дыр, находящихся в центрах галактик.

Характерные особенности гравитационных волн, возникающих при спиральном сближении объектов разных масс, неразрывно связаны с фундаментальными параметрами системы. Частота и амплитуда сигнала напрямую отражают массы компактных объектов — от звездных остатков до сверхмассивных черных дыр. Более того, вращение этих объектов, их спин, оказывает существенное влияние на форму генерируемой волны, создавая уникальные паттерны, позволяющие определить угловой момент системы. Анализ этих характеристик позволяет астрофизикам не только подтвердить существование этих экстремальных систем, но и точно измерить их параметры, углубляя понимание процессов, происходящих вблизи черных дыр и эволюции галактик. $f \propto \sqrt{\frac{M}{a^3}}$ , где $f$ — частота, $M$ — общая масса, а $a$ — большая полуось орбиты, демонстрирует прямую зависимость частоты от массы и обратную — от размера орбиты.

Продолжительность спирального сближения компактного объекта малой массы и сверхмассивной черной дыры, определяемая как инспиральный временной масштаб, играет ключевую роль в возможности обнаружения гравитационных волн и точности определения параметров системы. Этот временной масштаб подвержен влиянию космологической постоянной, что приводит к увеличению длительности сигнала и, как следствие, повышает вероятность его регистрации детекторами гравитационных волн. Более длительный сигнал позволяет с большей точностью измерить параметры объектов, такие как их массы и спины, а также характеристики орбиты. При этом, влияние космологической постоянной не только увеличивает продолжительность сигнала, но и усиливает эволюцию орбитальных параметров на протяжении всего процесса спирального сближения, предоставляя дополнительную информацию для астрофизического анализа и проверки космологических моделей.

Отношение временных шкал спирали Петерса-Мэтьюса и полной спирали SdS, зависящее от космологической постоянной и начальных параметров орбиты, демонстрирует, что более широкие орбиты испытывают более сильное влияние космологической постоянной, что приводит к более быстрому затуханию по сравнению с классическим временем затухания Петерса (<span class="katex-eq" data-katex-display="false"> \lambda = 0 </span>). — Отношение временных шкал спирали Петерса-Мэтьюса и полной спирали SdS, зависящее от космологической постоянной и начальных параметров орбиты, демонстрирует, что более широкие орбиты испытывают более сильное влияние космологической постоянной, что приводит к более быстрому затуханию по сравнению с классическим временем затухания Петерса ( $\lambda = 0$ ).

Исследование траекторий компактных бинарных систем в пространстве Шварцшильда-де Ситтера заставляет задуматься о природе кажущегося порядка. Авторы пристально изучают влияние космологической постоянной на эволюцию орбит, выявляя тонкие изменения в гравитационных волнах. Это напоминает о словах Конфуция: «Изучай прошлое, чтобы знать будущее». Подобно тому, как понимание предыдущих этапов эволюции системы позволяет предсказать её дальнейшую судьбу, так и анализ слабых сигналов гравитационных волн открывает путь к познанию Вселенной. В работе подчеркивается, что даже небольшие отклонения от классических моделей могут содержать важную информацию о фундаментальных свойствах пространства-времени.

Куда же дальше?

Представленная работа, исследуя влияние космологической постоянной на эволюцию компактных бинарных систем, лишь приоткрывает завесу над сложной игрой гравитации и расширяющейся Вселенной. Очевидно, что асимптотическое поведение орбит в пространстве Шварцшильда-де Ситтера, хотя и изучено, таит в себе нюансы, способные существенно повлиять на характеристики гравитационного излучения. Вопрос о точности адиабатического приближения, особенно на поздних стадиях спирали, требует более глубокого анализа — возможно, потребуется разработка новых методов, выходящих за рамки существующих.

Необходимо учитывать, что рассмотрение исключительно экстремальных масс-отношений — это, по сути, упрощение, позволяющее выявить ключевые эффекты. Реальные бинарные системы, вероятно, демонстрируют более сложное поведение, требующее численных симуляций, способных охватить широкий спектр масс и параметров. Кроме того, влияние спина компонентов на эволюцию орбит в пространстве де Ситтера остается практически неисследованным — это открывает плодотворное поле для будущих исследований.

И, наконец, стоит задуматься: не является ли космологическая постоянная лишь симптомом более глубокой, пока непостижимой, структуры Вселенной? Попытки связать динамику компактных бинарных систем с фундаментальными космологическими параметрами, возможно, приведут к неожиданным открытиям, заставляющим пересмотреть существующие модели гравитации. Проверка этих гипотез — задача не из легких, но именно в ней заключается истинный вызов для исследователя.

Оригинал статьи: https://arxiv.org/pdf/2602.17154.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-02-20 22:23