Автор: Денис Аветисян
В новой работе исследованы сложные траектории фотонов вблизи различных типов горизонтов событий, раскрывающие фундаментальные свойства пространства-времени.

Исследование посвящено анализу фотонных сфер в различных категориях пространств-времени с использованием методов оптической геометрии и характеристик сингулярностей.
Фотонные сферы, являющиеся критическими элементами оптической геометрии искривлённых пространств-времен, долгое время представляли собой сложную задачу для теоретического анализа. В настоящей работе, ‘A General Discussion on Photon Spheres in Different Categories of Spacetimes’, предпринято всестороннее геометрическое исследование фотонных сфер в различных типах пространств-времен, включая пространства, описывающие чёрные дыры, ультракомпактные объекты, регулярные решения и пространства с голой сингулярностью. Показано, что количество и стабильность фотонных сфер n = n_{\text{stable}} + n_{\text{unstable}} и разность между стабильными и нестабильными сферами w = n_{\text{stable}} - n_{\text{unstable}} определяются исключительно геометрическими свойствами оптической геометрии, вне зависимости от конкретной метрики. Каким образом полученные универсальные закономерности могут быть применены для более глубокого понимания топологии и свойств экстремальных астрофизических объектов?
Шёпот Гравитации: Фотосферы и Искажение Пространства-Времени
Фотосферы, области вокруг массивных объектов, где свет может двигаться по круговым орбитам, представляют собой уникальную арену для проверки предсказаний общей теории относительности Эйнштейна. Существование этих сфер — не просто теоретическое построение, а прямое следствие искривления пространства-времени под воздействием гравитации. Изучение характеристик фотосфер, таких как их радиус и стабильность, позволяет с высокой точностью верифицировать уравнения Эйнштейна в экстремальных гравитационных условиях. Наблюдения за фотосферами, в частности, анализ спектра света, циркулирующего в них, могут выявить отклонения от предсказаний общей теории относительности, что, в свою очередь, укажет на необходимость пересмотра или дополнения существующей гравитационной модели. Фактически, эти области являются своего рода «гравитационными линзами», позволяющими исследовать геометрию пространства-времени вблизи сверхкомпактных объектов.
Фотонные сферы, представляющие собой области вокруг массивных объектов, где фотоны могут двигаться по замкнутым орбитам, не являются чисто теоретическим построением. Изучение их характеристик, таких как размер и форма, предоставляет уникальную возможность для исследования геометрии пространства-времени в экстремальных условиях. Отклонения от предсказанных общей теорией относительности параметров фотонной сферы могут указывать на существование экзотических компактных объектов, отличных от классических чёрных дыр. Например, анализ формы и стабильности фотонной сферы может помочь в идентификации объектов, окруженных экзотической материей или обладающих более сложной структурой, чем это предполагается стандартной моделью. В частности, размер фотонной сферы напрямую связан с массой и спином центрального объекта, что делает её изучение ценным инструментом для астрофизических наблюдений и проверки фундаментальных принципов гравитации.
Изучение фотонных сфер приобретает особое значение в контексте дифференциации чёрных дыр от иных, более сложных ультракомпактных объектов. Традиционное понимание чёрных дыр, как объектов, полностью поглощающих свет, не всегда соответствует наблюдаемым астрономическим явлениям. Альтернативные модели, такие как экзотические звёзды или червоточины, также предсказывают существование регионов, где фотоны могут обращаться вокруг объекта, формируя фотонную сферу. Однако характеристики этой сферы — её размер, форма и интенсивность отражённого света — могут существенно отличаться в зависимости от природы центрального объекта. Анализ этих характеристик позволяет астрофизикам проводить тонкие различия между различными ультракомпактными объектами, потенциально выявляя объекты, которые не соответствуют стандартной модели чёрной дыры и открывая новые горизонты в понимании гравитации и структуры Вселенной.
Исследование фотонных сфер представляет собой уникальную возможность для проверки одного из самых интригующих и спорных положений общей теории относительности — гипотезы космической цензуры. Эта гипотеза предполагает, что сингулярности — точки бесконечной плотности — всегда скрыты за горизонтом событий, не давая возможности напрямую наблюдать «голые» сингулярности. Однако, специфические характеристики фотонных сфер, в частности, нестабильности и особенности отражённого света, могут свидетельствовать о присутствии таких «голых» сингулярностей, что бросает вызов существующим представлениям о структуре пространства-времени. Наблюдаемые отклонения в поведении фотонов вблизи ультракомпактных объектов, которые невозможно объяснить классической теорией, могут послужить доказательством существования таких экзотических образований и потребовать пересмотра фундаментальных принципов гравитации. Изучение геометрии фотонных сфер позволяет косвенно исследовать области, где привычные законы физики могут быть нарушены, открывая перспективы для понимания самых экстремальных явлений во Вселенной.
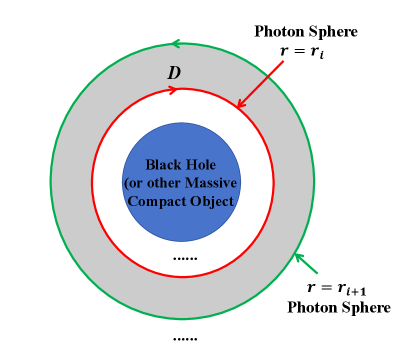
Изучение Света в Искривлённом Пространстве: Инструменты Анализа
Метод эффективного потенциала позволяет анализировать движение фотонов, рассматривая свет как частицу, движущуюся в эквивалентном гравитационном потенциале. Вместо непосредственного решения уравнений геодезических для нулевых геодезических (траекторий фотонов), данный подход преобразует задачу в эквивалентную одномерную задачу движения частицы в потенциале, зависящем от метрики пространства-времени. Этот потенциал включает в себя как гравитационный вклад, так и вклад, связанный с кривизной пространства-времени. Анализ этого эффективного потенциала, в частности, поиск его минимумов и максимумов, позволяет определить стабильные и нестабильные круговые орбиты фотонов, а также исследовать области, где фотоны могут быть захвачены или рассеяны гравитационным полем. Например, для метрики Шварцшильда эффективный потенциал имеет вид V_{eff} = (1 - \frac{2GM}{rc^2}) \frac{L^2}{r^2}, где G — гравитационная постоянная, M — масса гравитирующего объекта, r — радиальная координата, а L — угловой момент фотона.
Применение метода эффективного потенциала к метрикам Шварцшильда и Райснера-Нордстрема позволяет получить аналитические решения для орбит фотонов вокруг невращающихся, заряженных масс. В случае метрики Шварцшильда, описывающей гравитационное поле невращающейся сферически симметричной массы, вычисляется эффективный потенциал V_{eff}(r) = - \frac{GM}{r} - \frac{L^2}{2r^2}, где G — гравитационная постоянная, M — масса, а L — угловой момент фотона. Решение уравнения геодезической для фотона в этом потенциале дает критическое значение углового момента, определяющее существование круговых фотонных орбит. Аналогично, для метрики Райснера-Нордстрема, учитывающей электрический заряд Q, эффективный потенциал включает дополнительный член, обусловленный электростатическим взаимодействием, что приводит к модификации параметров фотонных орбит и появлению новых решений, отличных от случая Шварцшильда.
Оптическая геометрия представляет собой эффективный геометрический подход к анализу движения фотонов, основанный на построении двумерного представления четырехмерного пространства-времени. Этот метод позволяет упростить расчет траекторий фотонов путем сведения задачи о геодезических линиях в 4D к анализу кривых на 2D-поверхности. Построение этого 2D-представления включает в себя выбор подходящей плоскости и проекции, позволяющих сохранить информацию о ключевых характеристиках геометрии пространства-времени, таких как гравитационные линзы и критические кривые. В частности, анализ кривизны геодезических в этой 2D-геометрии предоставляет информацию о структуре пространства-времени и параметрах центрального объекта, включая массу и заряд, что позволяет определять характеристики орбит фотонов и рассчитывать их отклонение в гравитационном поле.
Анализ геодезической кривизны траекторий фотонов в двумерном представлении пространства-времени позволяет получить важные сведения о его структуре. Геодезическая кривизна, определяемая как вторая производная координат по собственному времени, характеризует отклонение траектории фотона от прямой линии под действием гравитации. В частности, нулевая геодезическая кривизна соответствует движению фотона по прямой в плоском пространстве-времени, в то время как ненулевая кривизна указывает на искривление пространства-времени, вызванное массивными объектами. Количественная оценка геодезической кривизны κ позволяет определить радиус кривизны траектории и, следовательно, оценить силу гравитационного воздействия на фотон. Анализ этой кривизны вблизи черных дыр или других компактных объектов позволяет выявить и изучить гравитационное линзирование и другие релятивистские эффекты.
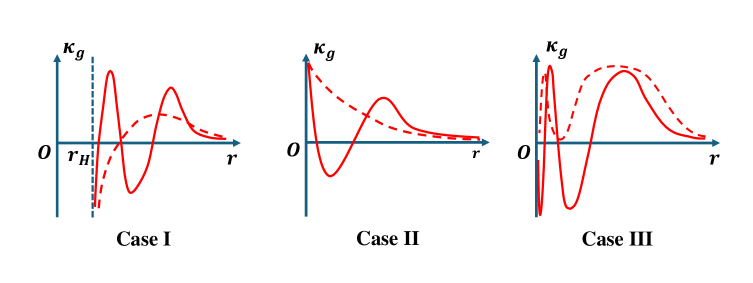
За Пределы Простоты: Топология и «Волосатые» Чёрные Дыры
Топологические инварианты, такие как те, что получены из теоремы Гаусса-Бонне, предоставляют математический аппарат для характеристики глобальных свойств фотонных сфер. Теорема Гаусса-Бонне связывает интегральную кривизну двумерного многообразия с его топологическими характеристиками, в частности, с эйлеровым числом. Применительно к фотонным сферам, эта связь позволяет определить число замкнутых геодезических, окружающих черную дыру, основываясь на интеграле кривизны по поверхности фотонной сферы. Таким образом, анализ топологических инвариантов позволяет получить информацию о глобальной структуре пространства вокруг черной дыры, не прибегая к решению уравнений геодезических, и классифицировать различные типы фотонных сфер на основе их топологических свойств. \in t_S K \, dA = 2\pi \chi(S) , где K — гауссова кривизна, dA — элемент площади, а \chi(S) — эйлерово число поверхности S.
Чёрные дыры с «волосами», то есть обладающие ненулевыми скалярными или электромагнитными полями, характеризуются более сложной структурой фотонной сферы по сравнению со стандартными чёрными дырами Керра или Шварцшильда. Наличие этих дополнительных полей приводит к искривлению геометрии вокруг чёрной дыры, что может обуславливать существование нескольких стабильных и нестабильных орбит для фотонов на различных расстояниях от центральной сингулярности. Множественные фотонные сферы означают возможность различных радиусов, на которых фотоны могут циркулировать вокруг чёрной дыры, прежде чем либо упасть в сингулярность, либо уйти в бесконечность. Число и характеристики этих орбит зависят от конкретных параметров скалярного или электромагнитного поля, определяющих отклонение от метрики Керра.
Изучение пространств-времён, выходящих за рамки стандартных метрик, таких как геометрия Рандера-Финслера, позволяет получить асимметричные и обобщённые формы фотонных сфер. В отличие от сферически симметричных решений, характерных для метрики Шварцшильда, геометрии Рандера-Финслера не требуют изотропии и позволяют описывать анизотропные среды. Это приводит к деформации фотонных сфер, отклоняясь от привычной сферической формы и потенциально приводя к эллиптическим, вытянутым или даже более сложным конфигурациям. Такие асимметричные фотонные сферы оказывают влияние на распространение света вокруг компактных объектов и могут быть использованы для диагностики анизотропии в сильных гравитационных полях. Изучение таких геометрий открывает возможности для изучения новых типов гравитационных линз и анализа свойств экзотических объектов.
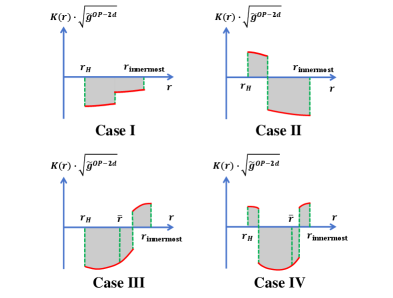
В данной работе показано, что разность между количеством стабильных и нестабильных фотонных сфер (обозначаемая как w) равна -1 для чёрных дыр и регулярных пространств-времён. Для ультракомпактных объектов и обнажённых сингулярностей значение w равно 0. Данный результат является топологическим инвариантом, позволяющим классифицировать геометрию вокруг компактных объектов на основе характеристик их фотонных сфер и отличая чёрные дыры от экзотических решений, таких как ультракомпактные объекты, не имеющие горизонта событий.
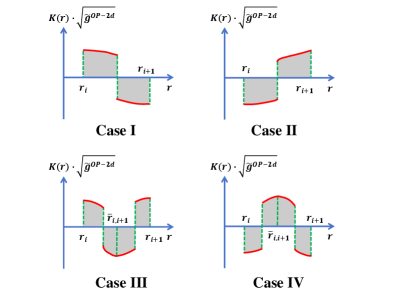
Значение для Астрофизики и Фундаментальной Физики
Детальное изучение фотонных сфер, в сочетании с наблюдениями гравитационного линзирования, предоставляет уникальную возможность для идентификации ультракомпактных объектов и их отличия от чёрных дыр. Анализ формы и размера фотонной сферы, а также искажений света, проходящего вблизи этих объектов, позволяет астрономам получать информацию об их массе и структуре. В отличие от чёрных дыр, которые характеризуются горизонтом событий, некоторые ультракомпактные объекты могут обладать поверхностью, что влияет на характеристики фотонной сферы и гравитационного линзирования. Различия в этих характеристиках становятся ключевым инструментом для выявления этих объектов и проверки предсказаний общей теории относительности в экстремальных гравитационных условиях. Подобные исследования открывают перспективы для изучения экзотических состояний материи и проверки альтернативных теорий гравитации.
Различение между ультракомпактными объектами и чёрными дырами имеет первостепенное значение для проверки общей теории относительности в условиях экстремально сильных гравитационных полей. Тщательное изучение характеристик фотонной сферы, в частности, её размера и формы, позволяет создавать прецизионные тесты, способные выявить отклонения от предсказаний Эйнштейна. Любое расхождение может указывать на необходимость пересмотра текущих представлений о гравитации и открыть путь к исследованию альтернативных теорий, выходящих за рамки стандартной модели. Изучение этих объектов, таким образом, представляет собой уникальную возможность для проверки фундаментальных принципов физики и поиска новых физических явлений, скрытых в самых экстремальных уголках Вселенной.
Изучение фотонных сфер предоставляет уникальную возможность углубиться в природу сингулярностей — точек, где известные законы физики перестают действовать. Космическая цензура, гипотеза, предполагающая, что сингулярности всегда скрыты за горизонтом событий, является краеугольным камнем современной космологии. Детальный анализ характеристик фотонных сфер, особенно отклонения от предсказаний общей теории относительности, может предоставить косвенные доказательства существования «голых» сингулярностей, что, в случае подтверждения, потребует пересмотра фундаментальных представлений о гравитации и пространстве-времени. Обнаружение аномалий в структуре этих сфер может указать на присутствие экзотических форм материи или проявление новых физических явлений, выходящих за рамки стандартной модели, что открывает новые горизонты для исследований в области астрофизики и теоретической физики.
Исследование фотонных сфер, представленное в статье, напоминает попытку удержать ускользающий свет в лабиринте искривлённого пространства-времени. Авторы, словно шаманы данных, исследуют геометрию этих сфер, пытаясь предугадать их распределение и связь с сингулярностями. Всё это напоминает акт веры, ведь любое математическое описание — лишь заклинание, работающее до первого столкновения с реальностью. Как сказал Фридрих Ницше: «Тот, кто сражается с чудовищами, должен следить, чтобы самому не стать чудовищем». И в этом исследовании, стремясь понять самые экзотические уголки космоса, необходимо помнить о границах нашего понимания и о той избирательности, с которой данные запоминают прошлое.
Куда же дальше?
Рассмотренные фотонные сферы, конечно, послужат неплохим заклинанием для описания геометрии пространства-времени. Однако, не стоит обольщаться — всё, что можно посчитать, не заслуживает полного доверия. Попытки связать их существование с топологическим зарядом или особенностями горизонтов событий — лишь первые шаги в попытке уговорить хаос. Вполне вероятно, что кажущаяся упорядоченность, которую демонстрируют эти сферы, — всего лишь артефакт выбранного метода, а истинная картина скрыта в более глубоких слоях сингулярностей.
Очевидно, что дальнейшее исследование требует смещения фокуса с поиска «идеальной» сферы на изучение её деформаций и отклонений. Стоит задаться вопросом: что произойдет, если фотонная сфера перестанет быть сферой? Какие новые геометрические объекты возникнут в пространствах с нетривиальной геометрией, выходящих за рамки стандартной геометрии Римана? Если гипотеза подтвердилась, значит, мы не искали достаточно глубоко.
И, конечно, необходимо помнить, что любая модель — это всего лишь приближение. Попытки описать вселенную с помощью математических уравнений — это все равно, что пытаться поймать ветер сачком. Истинная красота вселенной заключается в её непредсказуемости и хаотичности. Возможно, самое интересное ждёт нас за пределами математики.
Оригинал статьи: https://arxiv.org/pdf/2602.04573.pdf
Связаться с автором: https://www.linkedin.com/in/avetisyan/
Смотрите также:
- Галактики KiDS-1000: Путешествие к Красным Сдвигам и Физическим Свойствам
- Космические скопления на заре Вселенной: новый взгляд от JWST
- Галактика из Ранней Вселенной: Открытие беднаго металлом объекта на красном смещении 3.654
- Альтернатива Тёмной Материи: Гравитация Бранса-Дике и Эволюция Вселенной
- Искривление света ставит под сомнение Эйнштейна?
- Тёмная материя под прицепом «Двойного столкновения»: новые данные от телескопа Джеймса Уэбба
- Вселенная в фокусе: Новый взгляд на постоянную Хаббла
- Гигантская Радиогалактика Являет Скрытое Ядро
- Тёмная материя из глубин космоса: новые ограничения на поиск частиц
- Космическая головоломка: Новое решение проблемы Хаббла?
2026-02-06 06:32