Автор: Денис Аветисян
В данной работе исследованы особенности поведения кривизны пространства-времени в предельных случаях Калаби-Яу и предложен подход к разделению гравитационных эффектов.
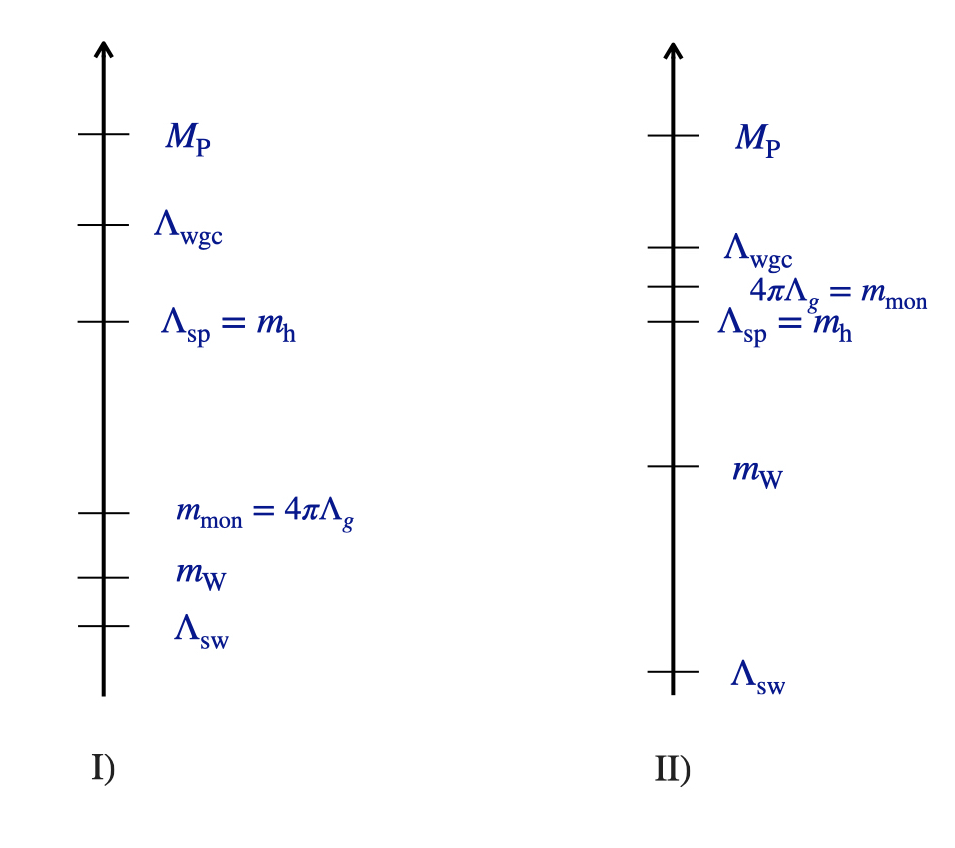
Исследование поведения кривизны и гравитационного разделения в предельных конфигурациях пространства Калаби-Яу.
В рамках теории струн и супергравитации, стремление к построению эффективных моделей в предельных случаях часто сталкивается с проблемой отделения гравитационных мод от негравитационных. В работе, посвященной ‘Curvature divergences and gravity decoupling in Calabi—Yau rigid limits’, исследуется этот эффект для компактификаций теории струн на многообразиях Калаби-Яу, акцентируя внимание на траекториях векторных мультиплетов с аксиальной симметрией. Показано, что выделение подмножества, так называемого «core RFT», возможно лишь при определенных условиях, связанных с расходимостью скалярной кривизны пространства модулей. Не приведет ли дальнейшее исследование этих расходимостей к более глубокому пониманию структуры пространства-времени в квантовой гравитации?
Разум и Модели: Ограничения Современных Языковых Сетей
Современные большие языковые модели (БЯМ) демонстрируют впечатляющие возможности в обработке естественного языка, успешно справляясь с задачами, требующими понимания и генерации текста. Однако, несмотря на кажущуюся интеллектуальность, подлинное рассуждение остаётся сложной проблемой. БЯМ превосходно распознают закономерности в данных, но часто испытывают трудности в ситуациях, требующих многоступенчатых логических выводов, анализа причинно-следственных связей и адаптации к новым, нестандартным задачам. В отличие от человеческого разума, способного к абстрактному мышлению и творческому решению проблем, БЯМ полагаются преимущественно на статистические закономерности, что ограничивает их способность к действительно глубокому пониманию и самостоятельному рассуждению.
Несмотря на впечатляющую способность к распознаванию закономерностей в больших объемах данных, современные языковые модели часто демонстрируют трудности в задачах, требующих последовательного логического вывода и надежного решения проблем. Вместо глубокого понимания принципов, они оперируют вероятностными связями, что приводит к ошибкам при решении задач, требующих нескольких этапов рассуждений или экстраполяции знаний на новые ситуации. Эта особенность ограничивает их применение в областях, где необходима не просто статистическая точность, а именно обоснованность и надежность принимаемых решений, таких как научные исследования или сложные инженерные расчеты. В таких контекстах, способность к многоступенчатому выводу является критически важной, и существующие модели пока не в состоянии обеспечить требуемый уровень достоверности.
Ограничения в способности к логическому мышлению существенно сдерживают внедрение больших языковых моделей в сферы, где необходимы надёжность и прозрачность рассуждений. В частности, это касается научных исследований, где требуется не просто выявление корреляций, но и понимание причинно-следственных связей, а также критически важных процессов принятия решений, например, в медицине или финансах. Отсутствие возможности чётко объяснить ход мыслей и обосновать сделанные выводы ставит под сомнение доверие к результатам, полученным с помощью таких моделей, и препятствует их использованию в ситуациях, где цена ошибки может быть очень высокой. Разработка методов повышения надёжности и объяснимости логических заключений представляется ключевой задачей для расширения области применения больших языковых моделей.
Стратегии Рассуждений: Как Выжать Максимум из Модели
Метод “Chain of Thought” (Цепочка Мыслей) заключается в стимулировании больших языковых моделей (LLM) к явному проговариванию промежуточных шагов рассуждений при решении задач. Вместо прямого предоставления ответа, LLM побуждается к последовательному изложению логики, ведущей к решению. Это повышает точность ответов, особенно в сложных задачах, требующих многоступенчатого анализа. Прозрачность процесса рассуждений также увеличивается, поскольку пользователь может отследить, как модель пришла к определенному выводу, что облегчает выявление и исправление ошибок. Использование данного подхода демонстрирует значительное улучшение производительности LLM в задачах, требующих арифметических вычислений, логического вывода и здравого смысла.
Метод «От простого к сложному» (Least-to-Most Prompting) предполагает последовательное решение сложной задачи путем её декомпозиции на ряд более простых, взаимосвязанных подзадач. Вместо прямой подачи сложного запроса, модели сначала предлагается решить базовые подзадачи, результаты которых затем используются как входные данные для решения последующих, более сложных этапов. Этот подход позволяет языковой модели преодолеть ограничения по объему контекста и вычислительным ресурсам, эффективно обрабатывая задачи, которые превышают её непосредственные возможности, за счет поэтапного накопления и применения знаний.
Дообучение моделей (Instruction Tuning) заключается в тонкой настройке больших языковых моделей (LLM) на специализированных наборах данных, содержащих примеры задач, требующих рассуждений. Этот процесс позволяет LLM не просто запоминать ответы, а усваивать принципы логического мышления и применять их к новым, ранее не встречавшимся задачам. В отличие от простого обучения с подкреплением, Instruction Tuning фокусируется на обучении модели следовать инструкциям и демонстрировать процесс рассуждений, что значительно улучшает обобщающую способность и надежность получаемых результатов, особенно в сложных когнитивных задачах.
Комбинация стратегий промптинга, таких как Chain of Thought и Least-to-Most, в сочетании с методами, как Program of Thought, направлена на структурирование процесса рассуждений больших языковых моделей (LLM). Program of Thought предполагает разделение задачи на последовательность логических шагов, которые LLM выполняет поэтапно, генерируя промежуточные результаты и обоснования для каждого шага. Это позволяет не только повысить надежность и точность ответов, но и обеспечивает возможность отслеживания и анализа логики, используемой моделью для решения задачи, что критически важно для сложных и критически важных приложений.
Проверка Рассуждений: От Арифметики к Сложному Выводу
Арифметическое рассуждение является важнейшим критерием оценки возможностей больших языковых моделей (LLM) в области логического вывода. Данный тип задач требует от модели не просто запоминания фактов, а выполнения точных математических операций и последовательного логического анализа. Оценка проводится по задачам, включающим сложение, вычитание, умножение, деление, а также более сложные операции, требующие применения порядка действий и анализа числовых рядов. Высокая точность в решении арифметических задач указывает на способность модели к последовательному и безошибочному выводу, что является фундаментальным аспектом общего интеллекта. Отсутствие ошибок в арифметических вычислениях служит базовым уровнем для оценки способности модели к более сложным формам рассуждения.
Оценка способности больших языковых моделей (LLM) к здравому смыслу (Commonsense Reasoning) и символьному мышлению (Symbolic Reasoning) выходит за рамки простых вычислений и позволяет определить их потенциал в применении общеизвестных знаний и абстрактных понятий. Задачи на здравый смысл требуют от модели понимания неявных предположений и контекста, а также способности делать логические выводы, основанные на реальном мире. Символьное мышление, в свою очередь, оценивает способность модели манипулировать абстрактными символами и отношениями, например, в задачах, связанных с логикой предикатов или решением аналогии. Успешное выполнение таких задач свидетельствует о более глубоком понимании модели, выходящем за рамки статистического сопоставления паттернов в данных обучения.
Многошаговые рассуждения (Multi-Hop Reasoning), требующие выполнения нескольких последовательных шагов логического вывода для получения ответа, часто выявляют слабые места больших языковых моделей (LLM) в обработке зависимостей на большом расстоянии и интеграции знаний. В таких задачах, модели сталкиваются с трудностями при поддержании когерентности информации на протяжении всей цепочки рассуждений, что приводит к ошибкам в промежуточных выводах и, как следствие, к неверным окончательным ответам. Сложность усугубляется необходимостью эффективно извлекать и комбинировать релевантную информацию из различных источников знаний, представленных в обучающих данных, и правильно применять её на каждом шаге рассуждения. Особенно проблематичны случаи, когда релевантная информация разбросана по большому объему текста или требует неявного вывода, что требует от модели более продвинутых способностей к пониманию контекста и логической дедукции.
Метод самосогласованности (Self-Consistency) представляет собой подход к оценке надежности больших языковых моделей (LLM), основанный на многократном генерировании цепочек рассуждений для одного и того же запроса. Вместо принятия первого полученного ответа, LLM генерирует несколько вариантов решения, а окончательный ответ определяется путем голосования или выбора наиболее часто встречающегося результата. Этот метод позволяет снизить влияние случайных ошибок в процессе рассуждений, поскольку ложные или неверные шаги, вероятно, будут отличаться в разных цепочках рассуждений и, следовательно, не будут доминировать в итоговом ответе. Эффективность самосогласованности особенно заметна в задачах, требующих сложных логических выводов и многошаговых рассуждений, где единичные ошибки могут привести к значительному отклонению от правильного решения.
Масштаб и Сложность: Будущее Рассуждений в Языковых Моделях
Масштаб языковых моделей играет ключевую роль в улучшении их способности к рассуждениям, предоставляя возможность захватывать и представлять сложные знания. Более крупные модели, содержащие миллиарды, а теперь и триллионы параметров, демонстрируют повышенную способность к обобщению, извлечению закономерностей и решению задач, требующих глубокого понимания контекста. Этот прогресс обусловлен тем, что увеличение масштаба позволяет модели хранить больше информации, выявлять тонкие взаимосвязи между понятиями и эффективно использовать накопленные знания при решении новых, ранее не встречавшихся проблем. По сути, масштаб модели определяет её «память» и способность к «мышлению», позволяя ей оперировать более сложными абстракциями и выполнять более сложные когнитивные операции.
Несмотря на то, что увеличение масштаба языковых моделей является важным фактором повышения их способности к рассуждениям, одного лишь этого недостаточно. Для максимальной реализации потенциала необходимы инновационные архитектурные решения и оптимизированные стратегии обучения. Простое увеличение числа параметров не гарантирует качественного улучшения способности модели к решению сложных задач, требующих логического вывода и обобщения знаний. Разработка новых архитектур, таких как модели, основанные на внимании или трансформаторы с усовершенствованными механизмами взаимодействия, позволяет более эффективно использовать вычислительные ресурсы и улучшить способность к анализу и синтезу информации. Параллельно с этим, оптимизация методов обучения, включая использование более качественных данных, алгоритмов регуляризации и техник обучения с подкреплением, позволяет модели быстрее и эффективнее осваивать сложные концепции и адаптироваться к новым задачам, что в конечном итоге приводит к значительному повышению ее способности к логическому мышлению и решению проблем.
Сложные задачи, требующие рассуждений, предъявляют к современным языковым моделям не только высокие требования к вычислительной мощности, но и необходимость интеграции информации из различных источников и адаптации к незнакомым ситуациям. Способность к синтезу знаний, полученных из гетерогенных данных, позволяет моделям формировать более полные и точные представления о мире, а умение адаптироваться к новым условиям — эффективно применять эти знания для решения нестандартных задач. Эффективное оперирование разнообразной информацией и гибкость в применении знаний являются ключевыми факторами, определяющими способность модели к глубокому и надежному рассуждению, что открывает перспективы для ее использования в сложных областях, где требуется не просто обработка данных, а именно понимание и адаптация к контексту.
Решение существующих проблем, связанных с масштабируемостью и сложностью больших языковых моделей, открывает путь к реализации их полного потенциала в критически важных областях. В перспективе это позволит использовать LLM не просто как генераторы текста, но и как надежных помощников в принятии решений, требующих глубокого анализа и логических выводов. Разработка моделей, способных к объяснению своих рассуждений и адаптации к новым ситуациям, имеет решающее значение для применения в таких областях, как медицина, финансы и научные исследования, где требуется не только результат, но и прозрачность процесса его получения. Подобный прогресс обещает трансформацию многих отраслей, предоставляя инструменты для решения сложных задач и повышения эффективности работы специалистов.
Представленная работа демонстрирует стремление к упрощению сложных систем, что находит отклик в философии Ричарда Фейнмана. Он говорил: «Если вы не можете объяснить что-то простыми словами, значит, вы сами этого не понимаете». Исследование, посвященное реализации логического кубита с использованием поверхностного кода на сверхпроводящих кубитах, направлено на снижение ошибок за счет кодирования информации. Это подобно хирургическому удалению избыточности, чтобы оставить лишь суть. Авторы, подобно умелым хирургам, стремятся к ясности в мире квантовых вычислений, где сложность может затмить фундаментальные принципы. Очевидно, что снижение логических ошибок является ключевым шагом к созданию надежных и масштабируемых квантовых компьютеров.
Куда же дальше?
Достижение снижения логических ошибок, продемонстрированное в данной работе, не является, конечно, финальной точкой. Скорее, это обнажение нового уровня сложности. Уменьшение ошибок — это всегда выявление тех, что остались. Теперь, когда физические недостатки всё более эффективно маскируются кодом, становится очевидной необходимость более глубокого понимания фундаментальных ограничений, заложенных в самой архитектуре кубитов. Недостаточно просто строить более «тихие» кубиты; необходимо понять, как их взаимодействие порождает новые формы ошибок.
Внимание, вероятно, сместится от совершенствования физических кубитов к разработке более элегантных кодов. Поиск кодов, требующих меньше физических кубитов для достижения той же степени защиты, станет ключевой задачей. Иронично, но простота может оказаться сложнее, чем изощренность. Удаление избыточности — это удаление защиты, и поиск баланса между этими двумя силами — это, возможно, самая сложная задача.
В конечном итоге, цель — не создание идеального кубита, а создание системы, устойчивой к его несовершенству. И в этом поиске, как и в любой скульптуре, суть не в том, что добавлено, а в том, что удалось убрать, оставив лишь самое необходимое.
Оригинал статьи: https://arxiv.org/pdf/2602.04957.pdf
Связаться с автором: https://www.linkedin.com/in/avetisyan/
Смотрите также:
- Галактики KiDS-1000: Путешествие к Красным Сдвигам и Физическим Свойствам
- Космические скопления на заре Вселенной: новый взгляд от JWST
- Галактика из Ранней Вселенной: Открытие беднаго металлом объекта на красном смещении 3.654
- Альтернатива Тёмной Материи: Гравитация Бранса-Дике и Эволюция Вселенной
- Искривление света ставит под сомнение Эйнштейна?
- Далекий маяк во Вселенной: обнаружен новый гамма-излучающий блазар
- Тёмная материя под прицепом «Двойного столкновения»: новые данные от телескопа Джеймса Уэбба
- Преодолевая гравитационные расхождения: Новый взгляд на предельные случаи Калаби-Яу
- Вселенная в фокусе: Новый взгляд на постоянную Хаббла
- Гигантская Радиогалактика Являет Скрытое Ядро
2026-02-07 19:29