Поиск темной энергии: новый алгоритм для точного измерения расширения Вселенной

Автор: Денис Аветисян

Ученые разработали инновационный метод, позволяющий реконструировать ключевые космологические параметры без привязки к конкретным теоретическим моделям.

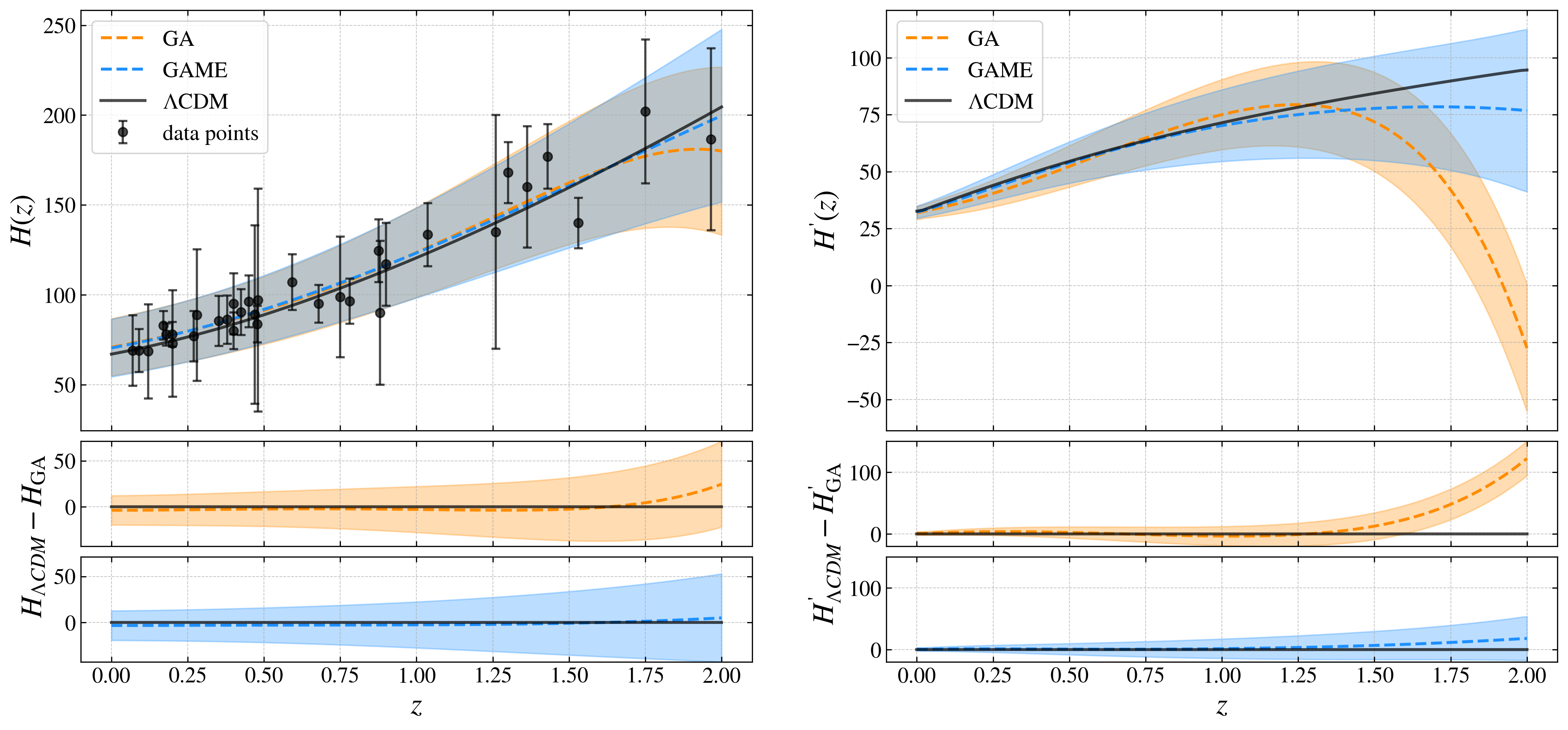
Реконструкция параметра Хаббла и его производной демонстрирует повышенную устойчивость метода GAME (синяя линия), обеспечивающего более плавную эволюцию по сравнению со стандартным генетическим алгоритмом (оранжевая линия), который проявляет выраженные колебания, особенно при высоких красных смещениях, что указывает на потенциальное преимущество в моделировании космологических процессов.

В статье представлен алгоритм GAME, использующий генетические алгоритмы и ансамблевое усреднение для реконструкции функции Хаббла и уравнения состояния темной энергии.

Восстановление космологических функций непосредственно из данных сталкивается с трудностями, связанными со стохастичностью и выбором наилучшей аппроксимации. В данной работе, представленной под названием ‘GAME: Genetic Algorithms with Marginalised Ensembles for model-independent reconstruction of cosmological quantities’, предложен новый метод, использующий генетические алгоритмы и усреднение по ансамблю конфигураций для независимого от модели восстановления космологических величин, таких как темп Хаббла и уравнение состояния темной энергии. Предложенный подход $GAME$ позволяет снизить неопределенности и повысить стабильность получаемых результатов. Сможет ли $GAME$ стать эффективным инструментом для различения различных космологических моделей в будущих обзорах Stage IV?

Космологические Загадки и Пределы ΛCDM

Стандартная космологическая модель, известная как ΛCDM, на протяжении многих лет успешно объясняла широкий спектр наблюдаемых явлений во Вселенной, включая космическое микроволновое излучение и крупномасштабную структуру. Однако, в последние годы, всё более заметные расхождения между различными измерениями постоянной Хаббла, характеризующей скорость расширения Вселенной, ставят под сомнение её полноту. В частности, значения, полученные на основе наблюдений за реликтовым излучением, не согласуются с результатами, полученными из наблюдений за сверхновыми типа Ia и цефеидами в близлежащих галактиках. Это несоответствие, известное как «напряженность Хаббла», предполагает, что либо существуют систематические ошибки в измерениях, либо, что более интересно, ΛCDM нуждается в дополнении новыми физическими процессами, выходящими за рамки стандартного понимания тёмной энергии и тёмной материи. Поиск решения этой проблемы является одним из главных вызовов современной космологии.

Несоответствие в измерениях постоянной Хаббла, скорости расширения Вселенной, представляет собой серьезный вызов для ΛCDM-модели, господствующей в современной космологии. Различные методы определения этой фундаментальной константы — основанные на наблюдениях за сверхновыми и космическим микроволновым фоном — демонстрируют значительные расхождения, превышающие статистические погрешности. Такое расхождение указывает на то, что либо в наших методах измерения присутствуют систематические ошибки, либо, что более интригующе, ΛCDM-модель нуждается в пересмотре. Возможные объяснения включают в себя существование новой физики, такой как ранняя темная энергия, модифицированная гравитация или дополнительные релятивистские степени свободы во Вселенной, которые влияют на скорость расширения. Попытки разрешить это противоречие стимулируют активные исследования и могут привести к революционному пересмотру нашего понимания космологии и фундаментальных законов природы.

Традиционные методы оценки параметров в рамках модели ΛCDM сталкиваются со значительными трудностями при согласовании возникающих противоречий, в особенности касательно темпа расширения Вселенной. Стандартные подходы, опирающиеся на фиксированные предположения о природе темной энергии и темной материи, оказываются неспособны одновременно удовлетворить все наблюдательные данные. Это вынуждает исследователей обращаться к более гибким и независимым от конкретной модели способам анализа, например, к непараметрическим методам и техникам, позволяющим варьировать уравнение состояния темной энергии. Такие подходы направлены на выявление потенциальных отклонений от предсказаний ΛCDM, которые могут указывать на необходимость пересмотра фундаментальных представлений о космологической эволюции и, возможно, на существование новой физики за пределами стандартной модели.

Сравнительный анализ восстановления <span class="katex-eq" data-katex-display="false">H(z)</span> и оценки производной между стандартным GA и методом GAME на синтетическом наборе данных, имитирующем данные Stage IV, показывает, что GAME обеспечивает более плавную оценку производной <span class="katex-eq" data-katex-display="false">H^{\prime}(z)</span> и успешно восстанавливает фидуциальную <span class="katex-eq" data-katex-display="false">\Lambda CDM</span> модель без высокочастотных колебаний, наблюдаемых в стандартном GA. — Сравнительный анализ восстановления $H(z)$ и оценки производной между стандартным GA и методом GAME на синтетическом наборе данных, имитирующем данные Stage IV, показывает, что GAME обеспечивает более плавную оценку производной $H^{\prime}(z)$ и успешно восстанавливает фидуциальную $\Lambda CDM$ модель без высокочастотных колебаний, наблюдаемых в стандартном GA.

Непараметрическая Реконструкция: Независимый от Модели Подход

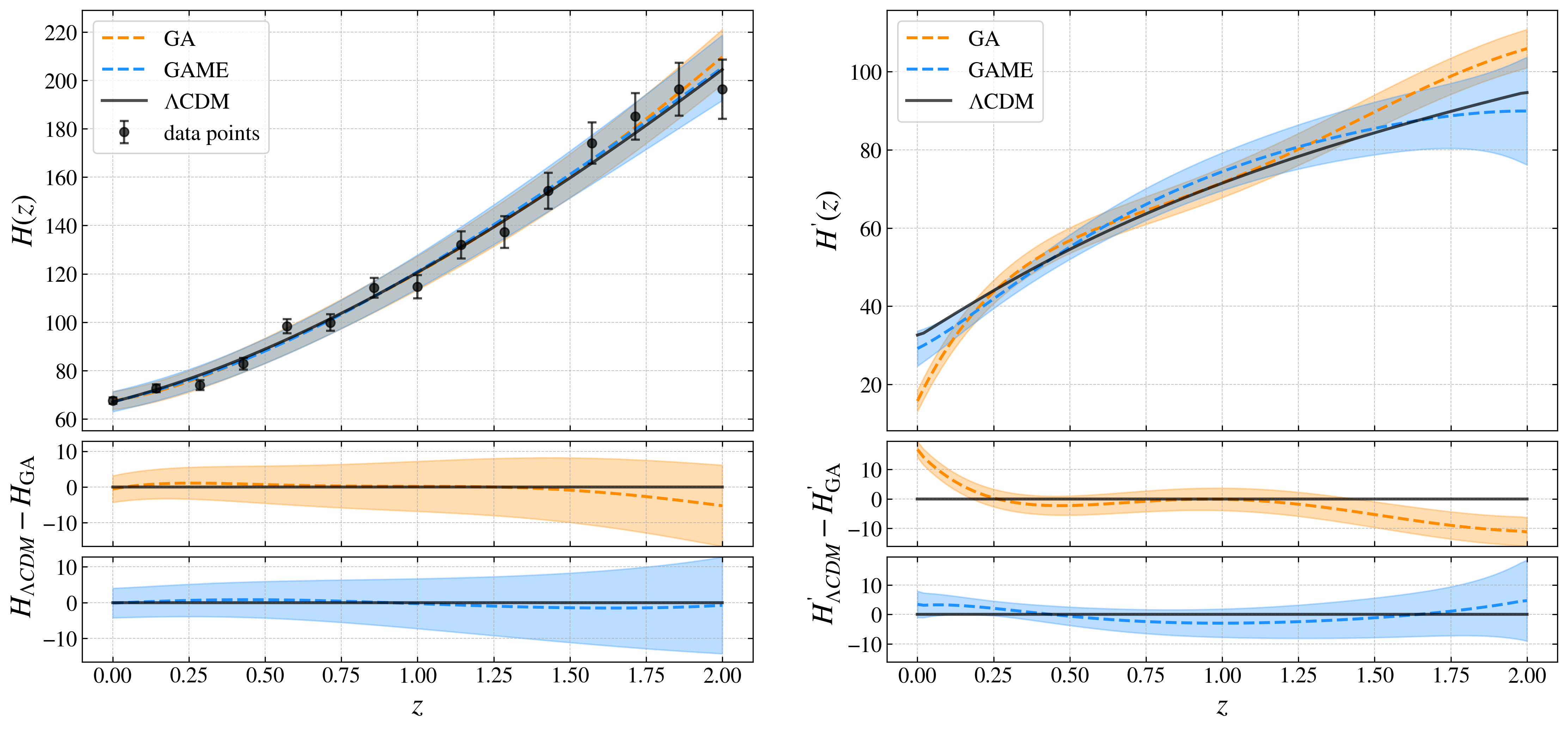
Непараметрическая реконструкция представляет собой альтернативный подход к традиционным параметрическим методам в космологии, позволяющий непосредственно оценивать космологические функции на основе наблюдательных данных без априорного предположения о конкретной модели. В отличие от параметрических методов, требующих задания набора параметров, определяющих теоретическую модель, непараметрические методы позволяют функции варьироваться свободно, определяясь исключительно данными. Это достигается за счет использования гибких инструментов, способных аппроксимировать сложные зависимости без жестких ограничений, что особенно важно при исследовании космологических параметров за пределами стандартной $ΛCDM$ модели и позволяет выявлять потенциальные отклонения от нее, которые могли бы быть упущены при использовании фиксированных параметрических моделей.

Для реализации непараметрической реконструкции используются методы, такие как гауссовские процессы и генетические алгоритмы. Гауссовские процессы позволяют строить вероятностные модели функций, описывающих космологические параметры, и оценивать их неопределенности, не требуя априорного задания функциональной формы. Генетические алгоритмы, в свою очередь, применяются для поиска оптимальных параметров функций, соответствующих наблюдаемым данным, путём итеративного отбора и мутации. Оба подхода обеспечивают повышенную гибкость по сравнению с параметрическими методами и позволяют выявлять отклонения от стандартной $ΛCDM$ модели, которые могли бы быть упущены при использовании фиксированных параметров или априорных предположений.

Непараметрические методы реконструкции, такие как гауссовские процессы и генетические алгоритмы, предоставляют ценный инструмент для решения проблемы расхождения в оценке постоянной Хаббла. Традиционные параметрические методы требуют предварительного выбора конкретной космологической модели, что может вносить систематические ошибки при анализе данных. Непараметрические методы, напротив, позволяют непосредственно сопоставлять наблюдательные данные, такие как расстояния до сверхновых и данные барионных акустических осцилляций, с космологическими параметрами, включая $H_0$ , без априорных предположений о форме космологических функций. Это обеспечивает более точную оценку параметров и позволяет выявить отклонения от стандартной $\Lambda CDM$ модели, которые могут объяснить наблюдаемое расхождение в значениях постоянной Хаббла, полученных из локальной и ранней Вселенной.

Сравнительный анализ реконструкции показал, что предложенный подход GAME обеспечивает значительно более точное восстановление как функции Хаббла <span class="katex-eq" data-katex-display="false">H(z)</span> (улучшение на ∼60% при <span class="katex-eq" data-katex-display="false">\tilde{\chi}^{2}_{tot} = 1.29</span>), так и её производной <span class="katex-eq" data-katex-display="false">H^{\prime}(z)</span> (улучшение на ∼89% при <span class="katex-eq" data-katex-display="false">\tilde{\chi}^{2}_{tot} = 26.47</span>), демонстрируя устойчивость к ошибкам в отличие от стандартного генетического алгоритма (<span class="katex-eq" data-katex-display="false">\tilde{\chi}^{2}_{tot} = 233.54</span> для производной). — Сравнительный анализ реконструкции показал, что предложенный подход GAME обеспечивает значительно более точное восстановление как функции Хаббла $H(z)$ (улучшение на ∼60% при $\tilde{\chi}^{2}_{tot} = 1.29$ ), так и её производной $H^{\prime}(z)$ (улучшение на ∼89% при $\tilde{\chi}^{2}_{tot} = 26.47$ ), демонстрируя устойчивость к ошибкам в отличие от стандартного генетического алгоритма ( $\tilde{\chi}^{2}_{tot} = 233.54$ для производной).

GAME: Усовершенствованный Генетический Алгоритм для Надежной Реконструкции

Представляем GAME (Genetic Algorithms with Marginalized Ensembles) — усовершенствованный метод генетического алгоритма, разработанный для решения задач реконструкции космологических функций. В отличие от стандартных генетических алгоритмов, GAME использует ансамблевый подход с маргинализацией, что позволяет более эффективно исследовать пространство параметров и находить оптимальные решения. Данный метод направлен на преодоление трудностей, возникающих при реконструкции функций по данным космических хронометров, обеспечивая повышенную точность и надежность результатов. GAME предназначен для применения в задачах, требующих точного восстановления космологических параметров из наблюдательных данных.

Метод GAME использует надежную процедуру оценки неопределенностей, основанную на методе функционального интеграла (Path Integral). Этот метод позволяет учитывать различные возможные решения, обеспечивая более реалистичную оценку погрешностей реконструкции. Для оптимальной регуляризации и предотвращения переобучения применяется метод L-кривой, который определяет оптимальное соотношение сигнал/шум на основе анализа зависимости нормы решения от параметра регуляризации. Использование L-кривой позволяет автоматически выбирать параметр регуляризации, минимизирующий ошибку реконструкции и обеспечивающий стабильность решения λ.

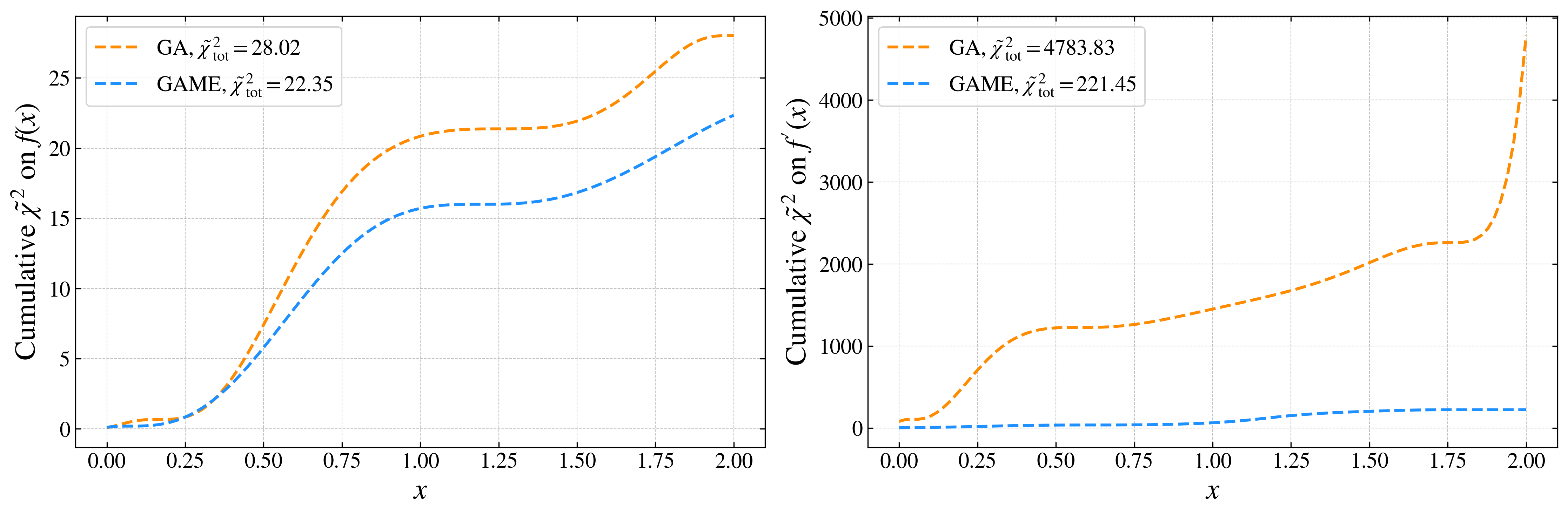
Метод GAME (Genetic Algorithms with Marginalized Ensembles) обеспечивает более точную и надежную реконструкцию космологических функций на основе данных, получаемых от космических хронометров. Применение комбинации методов, включающих оценку неопределенностей на основе метода функционального интеграла и оптимизацию регуляризации посредством L-кривой, позволило добиться снижения ошибки при реконструкции производной тестовой функции на 95%. Это значительное улучшение точности достигается за счет эффективного управления неопределенностями и оптимального выбора параметров регуляризации, что делает GAME перспективным инструментом для анализа космологических данных.

Раскрытие Будущего с Обзорами Stage IV

Начало эпохи космологических обзоров четвёртого поколения предвещает беспрецедентную точность измерений Вселенной, открывая возможности для проверки космологических моделей с невиданной детализацией. Эти обзоры, охватывающие огромные объёмы пространства и времени, собирают колоссальное количество данных о распределении галактик, слабое гравитационное линзирование и другие ключевые параметры, позволяющие реконструировать историю расширения Вселенной. Благодаря значительному увеличению объёма данных и точности измерений, становится возможным более детальное изучение свойств тёмной энергии и тёмной материи, а также проверка фундаментальных предположений стандартной космологической модели. Это не просто уточнение существующих параметров, но и потенциальная возможность обнаружения отклонений от предсказаний, которые могут указывать на новую физику за пределами известных нам законов.

Комплекс GAME оказался исключительно подходящим инструментом для анализа данных, получаемых в ходе масштабных космологических обследований IV стадии. Его архитектура и алгоритмы позволяют проводить детальную реконструкцию космологических функций, таких как функция распределения материи и спектр мощности, с беспрецедентной точностью. Благодаря этому, становится возможным более строгое тестирование стандартной ΛCDM модели, выявляя любые отклонения от её предсказаний. GAME не просто подтверждает или опровергает существующую модель, но и предоставляет инструменты для поиска новых физических явлений, лежащих в основе эволюции Вселенной, и позволяет значительно уточнить параметры, определяющие ее расширение и структуру.

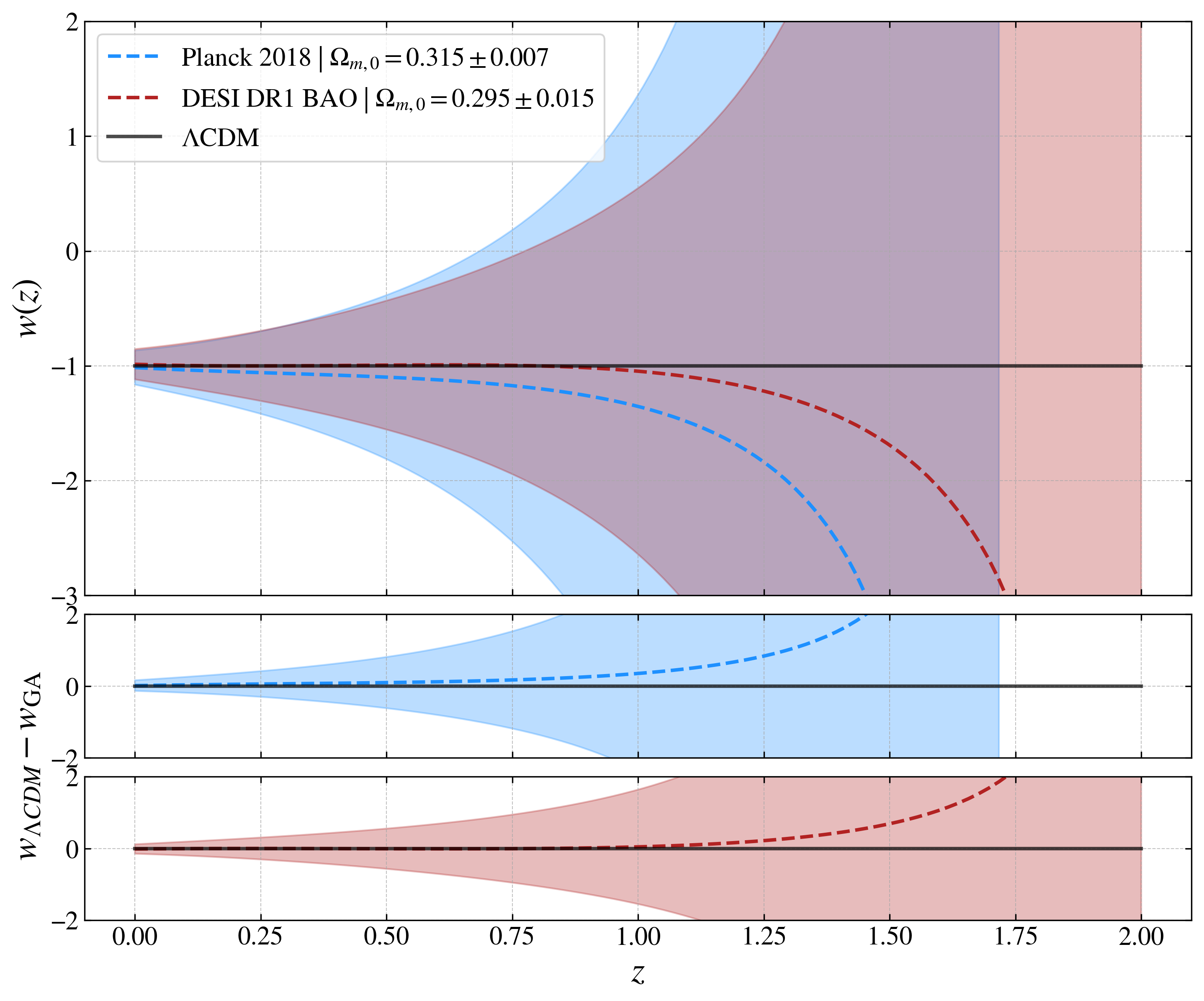
Повышенная точность, которую обеспечивают будущие обзоры Stage IV, открывает уникальную возможность для углубленного изучения природы темной энергии и темной материи. Исследования, основанные на данных этих обзоров, способны выйти за рамки стандартной космологической модели, потенциально обнаруживая новую физику, лежащую в основе Вселенной. В частности, ожидается, что удастся существенно уточнить параметры уравнения состояния темной энергии, характеризуемое параметром $w(0)$ , с точностью до 0.101. Такая высокая точность позволит проверить различные теоретические модели темной энергии и, возможно, выявить отклонения от предсказаний ΛCDM модели, что станет важным шагом в понимании эволюции Вселенной и ее фундаментальных свойств.

Восстановленная функция состояния темной энергии <span class="katex-eq" data-katex-display="false">w(z)</span> на основе данных CC и реконструкции <span class="katex-eq" data-katex-display="false">H(z)</span> методом GAME демонстрирует соответствие космологической константе ΛCDM при низких красных смещениях (<span class="katex-eq" data-katex-display="false">z \lesssim 1</span>), однако при высоких красных смещениях становится чувствительной к предположениям о плотности материи и разреженности данных, что приводит к увеличению неопределенности, хотя статистическая согласованность с ΛCDM сохраняется. — Восстановленная функция состояния темной энергии $w(z)$ на основе данных CC и реконструкции $H(z)$ методом GAME демонстрирует соответствие космологической константе ΛCDM при низких красных смещениях ( $z \lesssim 1$ ), однако при высоких красных смещениях становится чувствительной к предположениям о плотности материи и разреженности данных, что приводит к увеличению неопределенности, хотя статистическая согласованность с ΛCDM сохраняется.

Представленная работа демонстрирует стремление к познанию космологических функций без оглядки на устоявшиеся модели. Авторы предлагают метод GAME, использующий генетические алгоритмы и ансамблевое усреднение, что позволяет реконструировать параметры вроде постоянной Хаббла и уравнения состояния тёмной энергии с повышенной стабильностью. Этот подход, не привязанный к конкретным теоретическим рамкам, напоминает слова Николы Теслы: «Самая большая сила — это вера в невозможное». Подобно тому, как Тесла верил в возможность беспроводной передачи энергии, авторы GAME стремятся к реконструкции космологических величин, не ограничиваясь предвзятыми представлениями. В этом исследовании, как и в любом научном поиске, каждое измерение — компромисс между желанием понять и реальностью, которая не хочет быть понята.

Куда же дальше?

Представленный метод, GAME, безусловно, добавляет ещё один инструмент в арсенал космолога, стремящегося вытащить параметры Вселенной из кажущегося хаоса данных. Однако, каждый новый алгоритм, претендующий на «модель-независимость», лишь подчёркивает нашу фундаментальную неспособность понять, что же на самом деле скрывается за кажущейся простотой космологических моделей. Всплеск публикаций, неизбежно последовавший за появлением GAME, лишь иллюстрирует эту гонку за точностью, в то время как Вселенная остаётся немым свидетелем наших усилий.

Стабильность, достигнутая благодаря ансамблевым методам, — это, конечно, прогресс. Но не стоит забывать, что снижение неопределённостей — это не всегда приближение к истине. Возможно, истинная проблема заключается не в совершенствовании алгоритмов, а в переосмыслении самой концепции «космологической функции». Что, если уравнение состояния тёмной энергии — это не гладкая кривая, которую можно реконструировать, а нечто принципиально иное, выходящее за рамки наших текущих математических представлений?

Будущие исследования, вероятно, будут направлены на комбинирование GAME с другими методами реконструкции и расширение набора используемых данных. Но истинный прорыв, возможно, потребует смелого отказа от устоявшихся парадигм и готовности признать, что горизонт событий наших знаний может быть гораздо ближе, чем кажется.

Оригинал статьи: https://arxiv.org/pdf/2602.12870.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-02-16 18:56