Автор: Денис Аветисян
Исследование показывает, что в рамках модифицированной теории гравитации f(Q,T) возможно построение проходимых кротовых нор, не требующих использования экзотической материи.
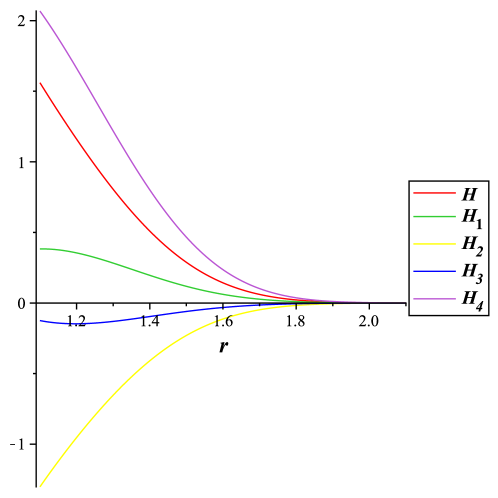
В статье представлены решения для проходимых кротовых нор в f(Q,T) гравитации, обходящие необходимость в нарушении стандартных энергетических условий.
Поиск решений уравнений гравитации, допускающих существование проходимых червоточин, традиционно сталкивается с необходимостью введения экзотической материи, нарушающей стандартные энергетические условия. В данной работе, посвященной исследованию ‘Non-exotic asymptotically flat wormholes in $f(Q,T)$ gravity’, рассматривается возможность построения решений, описывающих червоточины, в рамках модифицированной гравитации f(Q,T), где Q — неметричность, а T — след тензора энергии-импульса. Показано, что за счет учета связи между неметричностью и материей, удается найти широкий класс решений, допускающих существование проходимых червоточин без необходимости в экзотической материи, при этом сохраняется асимптотическая плоскостность пространства-времени. Каковы перспективы дальнейшего изучения влияния неметричности на структуру пространства-времени и возможность создания стабильных червоточин в рамках данной теории?
Червоточины: Вызов Стандартной Модели Вселенной
Червоточины, представляющие собой гипотетические туннели сквозь пространство-время, бросают вызов фундаментальным принципам общей теории относительности Эйнштейна. Представление о возможности существования таких структур требует пересмотра устоявшихся представлений о гравитации и её взаимодействии с материей. В рамках этой теории, червоточины не просто экзотические решения уравнений, но и индикаторы пределов применимости самой модели, поскольку их существование ставит под вопрос привычные представления о причинности и топологии пространства-времени. Изучение червоточин, таким образом, является не только поиском путей для гипотетических межзвездных путешествий, но и углубленным исследованием границ нашего понимания Вселенной и гравитационных сил, определяющих её структуру.
Традиционные решения, описывающие существование кротовых нор, сталкиваются с серьезной проблемой, требующей наличия так называемой «экзотической материи». Данное вещество характеризуется отрицательной плотностью энергии, что противоречит всем известным и подтвержденным энергетическим условиям, лежащим в основе современной физики. Это означает, что для поддержания стабильности и проходимости кротовой норы необходима материя, обладающая свойствами, которые не наблюдаются в привычном нам мире и даже кажутся физически невозможными. Использование экзотической материи ставит под сомнение саму возможность существования кротовых нор в реальности, а также требует пересмотра фундаментальных представлений о гравитации и структуре пространства-времени. Исследования в этой области направлены на поиск альтернативных теоретических моделей, которые могли бы обойтись без необходимости в столь необычном веществе, или же предложить механизмы, позволяющие стабилизировать кротовые норы с использованием известных форм материи.
Существование червоточин, как теоретических туннелей в пространстве-времени, тесно связано с решениями уравнений Эйнштейна — фундаментальных уравнений общей теории относительности. Однако, поиск стабильных и проходимых червоточин в рамках этих уравнений наталкивается на значительные трудности, требуя введения экзотической материи с отрицательной плотностью энергии. Это обстоятельство указывает на необходимость рассмотрения альтернативных теоретических рамок, выходящих за пределы стандартной общей теории относительности. Исследователи активно изучают модифицированные теории гравитации, такие как теории с дополнительными измерениями или некоммутативной геометрией, в надежде найти решения, которые позволят объяснить существование червоточин без прибегания к физически неправдоподобным предположениям о свойствах материи. Подобные исследования открывают перспективы для углубленного понимания структуры пространства-времени и природы гравитации, а также для поиска новых физических принципов, лежащих в основе Вселенной.
Обеспечение проходимости кротовых нор представляет собой сложную задачу, требующую детального изучения взаимодействия геометрии пространства-времени и материи. Теоретические расчеты показывают, что для предотвращения мгновенного схлопывания туннеля необходимы не только экзотические формы материи с отрицательной плотностью энергии, но и точное управление гравитационными силами внутри и вокруг горловины. Исследования в этой области фокусируются на поиске стабильных конфигураций пространства-времени, которые могли бы поддерживать открытое состояние кротовой норы, несмотря на колоссальное гравитационное давление. Особое внимание уделяется изучению влияния различных типов материи на кривизну пространства-времени и разработке моделей, описывающих динамику и стабильность таких структур. Понимание этих взаимосвязей имеет решающее значение для оценки физической реализуемости кротовых нор и их потенциальной роли в межзвездных путешествиях или других гипотетических приложениях.
f(Q,T) Гравитация: Новый Геометрический Подход
Гравитация f(Q,T) представляет собой расширение общей теории относительности, включающее в свою динамику неметричность Q и след тензора энергии-импульса T. В рамках этой теории, гравитационное взаимодействие определяется не только метрикой пространства-времени, как в общей теории относительности, но и этими дополнительными геометрическими и физическими величинами. Неметричность характеризует изменение длины векторных связей при параллельном переносе, а след тензора энергии-импульса отражает плотность энергии и давления материи. Включение этих величин в гравитационные уравнения позволяет описывать гравитационные эффекты, которые не могут быть объяснены в рамках стандартной общей теории относительности, и предлагает альтернативный подход к моделированию гравитационных явлений.
Модификация общей теории относительности в рамках f(Q,T)-гравитации вводит понятие ‘эффективного напряжения’, возникающего вследствие связи между геометрией пространства-времени и материей. В отличие от традиционных решений, требующих наличия экзотической материи с отрицательной плотностью энергии для поддержания, например, проходимых решений в геометрии червоточин, f(Q,T)-гравитация позволяет получать такие решения без привлечения экзотической материи. Это достигается за счет вклада неметричности Q и следа тензора энергии-импульса T в уравнения гравитации, которые генерируют дополнительное напряжение, компенсирующее гравитационное отталкивание, необходимое для поддержания открытой геометрии.
Теория f(Q,T) гравитации использует понятие неметричности Q для модификации геометрии пространства-времени, предлагая альтернативный механизм по сравнению со стандартной общей теорией относительности. В отличие от метрических теорий гравитации, где изменения геометрии напрямую связаны с энергией-импульсом, неметричность позволяет изменять кривизну без нарушения условий энергетической плотности. Это достигается за счет включения в уравнения гравитации не только метрического тензора, но и тензора неметричности, что позволяет генерировать эффективное напряжение, способное искривлять пространство-время без необходимости в экзотической материи с отрицательной плотностью энергии. Таким образом, f(Q,T) гравитация предоставляет возможность манипулировать геометрией пространства-времени, сохраняя при этом соответствие физически обоснованным энергетическим условиям.
Теория f(Q,T)-гравитации предлагает новый подход к достижению условий, необходимых для формирования и стабильности червоточин, решая тем самым ряд давних теоретических проблем. Традиционные решения для поддержания проходимых червоточин требуют существования экзотической материи, нарушающей различные энергетические условия. Однако, используя неметричность Q и след тензора энергии-импульса T в качестве динамических величин, данная теория позволяет генерировать эффективное напряжение, способное поддерживать геометрию червоточины без необходимости в экзотической материи. Это достигается за счет модификации уравнений Эйнштейна, что позволяет находить решения, удовлетворяющие требованиям стабильности и проходимости, и потенциально открывает новые возможности для изучения топологически нетривиальных пространств-времен.
Решения Червоточин в f(Q,T) Гравитации: Путь к Реальности
Решения модифицированных уравнений Эйнштейна в рамках ф(Q,T) гравитации демонстрируют возможность построения геометрий, соответствующих проходимым червоточинам. В отличие от традиционных подходов, требующих введения экзотической материи с отрицательной плотностью энергии, ф(Q,T) гравитация позволяет получать решения, описывающие червоточины, удовлетворяющие стандартным энергетическим условиям. Это достигается за счет модификации гравитационного взаимодействия, обусловленной неметрической связностью Q и скалярной кривизной T, что приводит к появлению дополнительных членов в уравнениях поля, компенсирующих гравитационное притяжение и позволяющих поддерживать открытое горло червоточины без необходимости привлечения экзотической материи.
В рамках теории гравитации f(Q,T) были получены решения, позволяющие построить геометрии червоточин без необходимости введения экзотической материи. Традиционно, для поддержания открытого горла червоточины требовались гипотетические формы материи с отрицательной плотностью энергии. Однако, решения уравнений поля Эйнштейна в модифицированной форме f(Q,T) демонстрируют возможность создания проходимых червоточин, удовлетворяющих условиям физической реальности и стабильности, при соблюдении определенных параметров, таких как α/(1+β) < 0 , что позволяет избежать необходимости в экзотической материи и представляет собой значительный прогресс в данной области исследований.
Геометрия червоточин, получаемых в рамках f(Q,T) гравитации, определяется функцией формы (shape function), которая математически описывает конфигурацию горловины червоточины и, следовательно, её проходимость. Данная функция, обозначаемая обычно как r(z), задает радиальную зависимость геометрии пространства-времени и определяет размер и форму горловины. Проходимость червоточины напрямую связана с условиями, накладываемыми на функцию формы, в частности, с требованием конечности кривизны и отсутствия сингулярностей в горловине. Анализ функции формы позволяет оценить геодезическую проходимость, то есть возможность существования траекторий, проходящих через горловину без нарушения каузальности и без столкновения с сингулярностями.
Для обеспечения физической реалистичности и стабильности решений, описывающих проходимые червоточины в рамках гравитации f(Q,T), необходимо соблюдение ряда ключевых параметров. Асимптотическая плоскостность гарантирует, что геометрия червоточины переходит в плоское пространство на больших расстояниях, что соответствует наблюдаемым космологическим данным. Условие “горловины” (throat condition) определяет геометрию окрестности горловины червоточины, предотвращая сингулярности и обеспечивая конечный размер горловины. Особенно важно, что для получения решений, не требующих экзотической материи, необходимо выполнение неравенства α / (1 + β) < 0, где α и β — параметры, характеризующие форму функции и тензор энергии соответственно. Соблюдение этих параметров критически важно для построения физически обоснованных моделей проходимых червоточин.
Геометрические Ограничения и Проходимость Червоточин
Функция красного смещения играет ключевую роль в определении энергетических затрат на прохождение через червоточину. Данная функция описывает изменение частоты фотонов, испытывающих гравитационное воздействие при приближении к горловине червоточины, что проявляется как увеличение длины волны — красное смещение. Чем сильнее гравитация вблизи горловины, тем значительнее красное смещение, и, следовательно, тем больше энергии требуется наблюдателю для преодоления этого гравитационного воздействия и прохождения через червоточину. В рамках теории гравитации f(Q,T), анализ функции красного смещения позволяет установить ограничения на геометрию пространства-времени, необходимые для обеспечения проходимости червоточины, и определить минимальный энергетический порог, необходимый для безопасного путешествия через неё. z = \frac{\nu_e}{\nu_o} - 1 — эта формула количественно описывает величину красного смещения, где \nu_e — частота излучения у источника, а \nu_o — частота, наблюдаемая удалённым наблюдателем.
Условие «расширения», связанное с функцией формы, определяет, останется ли горловина червоточины открытой для прохождения. Исследования показывают, что для обеспечения проходимости необходимо, чтобы показатель степени закона степенной функции формы был меньше единицы (n < 1). Этот критерий обусловлен геометрией пространства-времени вблизи горловины; если показатель степени превышает единицу, гравитационные силы будут стремиться к схлопыванию горловины, делая прохождение невозможным. Таким образом, значение n является ключевым параметром, определяющим, является ли теоретическая червоточина действительно проходимой, и играет решающую роль в исследовании возможности межзвездных путешествий в рамках данной теоретической модели.
Установление линейного уравнения состояния для материи, находящейся внутри червоточины, играет ключевую роль в анализе стабильности полученного решения. Данное уравнение, связывающее давление и плотность материи p = \omega \rho, где ω — константа, позволяет исследовать, насколько устойчива геометрия червоточины к малым возмущениям. Подобный подход упрощает математический анализ и позволяет выявить условия, при которых червоточина сохраняет свою проходимость, не коллапсируя под действием гравитационных сил. Использование линейного уравнения состояния является важным шагом в определении физической реализуемости и долгосрочной стабильности гипотетических червоточин в рамках теории гравитации f(Q,T).
Исследования в рамках f(Q,T)-гравитации показывают, что существование проходимых червоточин тесно связано с определенными геометрическими и физическими ограничениями. Эти ограничения не просто математические условия, но и фундаментальные требования к структуре пространства-времени и природе материи, поддерживающей червоточину. В частности, необходимо соблюдение условий, касающихся функции красного смещения F(r) и формы пространства вокруг горловины червоточины, определяемой показателем степени n в законе степеней. Для обеспечения проходимости червоточины, значение n должно быть меньше единицы, что указывает на необходимость экзотической материи с отрицательной плотностью энергии. Кроме того, установление линейного уравнения состояния для материи внутри червоточины позволяет анализировать стабильность решения и подтверждает, что лишь при соблюдении этих взаимосвязанных ограничений, червоточина может оставаться открытой и пригодной для прохождения, представляя собой теоретически возможный путь для межзвездных путешествий.
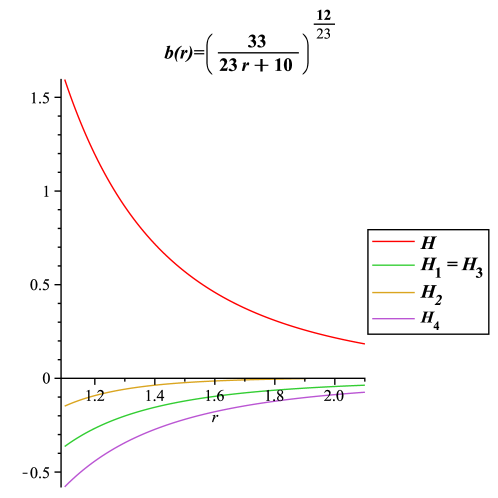
Исследование, представленное в данной работе, демонстрирует, что архитектура пространства-времени, описываемая в рамках $f(Q,T)$ гравитации, может быть более устойчивой и гибкой, чем предполагалось ранее. Особое внимание уделяется возможности создания проходимых червоточин без необходимости в экзотической материи, что является значительным шагом в понимании топологии пространства. В этом контексте, слова Галилея: «Все системы стареют — вопрос лишь в том, делают ли они достойно» приобретают особую актуальность. Подобно тому, как системы со временем изменяются, так и пространственно-временные структуры могут эволюционировать и адаптироваться, сохраняя при этом свою функциональность и проходимость, даже при отсутствии нестандартных форм материи. Устойчивость и долговечность решений, предлагаемых в статье, подчеркивают, что время является не просто метрикой, а средой, в которой эти системы существуют и развиваются.
Что впереди?
Исследование, представленное в данной работе, лишь слегка отодвигает завесу над сложной взаимосвязью между геометрией пространства-времени и его материальным содержанием. Обнаружение проходимых решений червоточин в рамках $f(Q,T)$ гравитации, не требующих экзотической материи, конечно, заманчиво. Однако, подобно любому временному явлению, эти решения существуют лишь в определенном контексте. Вопрос не в том, возможно ли существование червоточин, а в том, насколько устойчива эта возможность во времени, и каковы ее пределы.
Логирование, то есть хроника жизни системы, указывает на необходимость дальнейшего изучения динамической стабильности полученных решений. Развертывание, это мгновение на оси времени, требует детального анализа возмущений и их влияния на проходимость червоточины. Ограничения, связанные с конкретным выбором функции $f(Q,T)$, требуют расширения поиска и разработки более общих моделей, способных описывать широкий спектр физических сценариев.
В конечном счете, все системы стареют — вопрос лишь в том, делают ли они это достойно. Следующим шагом видится не просто поиск новых решений, а разработка инструментов для оценки их физической правдоподобности и долговечности. Понимание того, как гравитация взаимодействует с неметричностью и материей, остаётся ключом к разгадке тайн Вселенной, и каждое новое исследование — лишь новая глава в этой бесконечной истории.
Оригинал статьи: https://arxiv.org/pdf/2602.00527.pdf
Связаться с автором: https://www.linkedin.com/in/avetisyan/
Смотрите также:
- Галактики на карте звёздообразования: новый взгляд на эволюцию
- Массивные галактики на заре Вселенной: JWST подтверждает стандартную модель
- Космическая паутина и скрытые сигналы: очистка реликтового излучения от искажений
- Нейтрино: Посланники из Глубин Космоса
- Сверхяркие рентгеновские источники: Радиосигналы из глубин галактик
- Тёмная энергия: новый взгляд на ускорение Вселенной
- Ранняя Вселенная: Как рождались первые галактики
- Тёмная энергия: взгляд сквозь призму наблюдений
- Тень чёрной дыры: как космология влияет на её форму
- Небо в лучах гамма: 11 лет наблюдений за мимолетными вспышками
2026-02-04 03:43