Автор: Денис Аветисян
Новое исследование показывает, что вращение играет ключевую роль в динамике сверхтекучих полей в космологических моделях, потенциально изменяя их уравнение состояния.
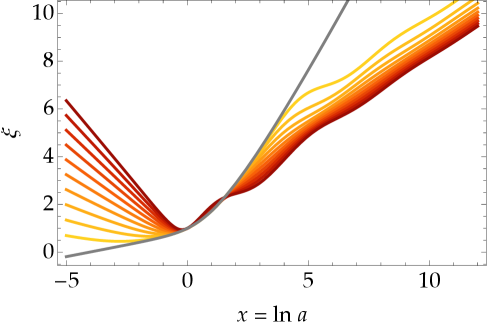
Работа посвящена исследованию космологических сценариев с движущимися сверхтекучими средами, описываемыми скалярными полями со сдвиговой симметрией, и анализу влияния вращения на их эволюцию.
Несмотря на успехи в моделировании космологических сценариев, вопрос о роли вращения в эволюции вселенной остается недостаточно изученным. В работе ‘Moving superfluids in the rotating universe’ исследуются однородные космологические модели, включающие сверхтекучие скалярные поля, демонстрирующие, что вращение становится существенным динамическим фактором на поздних стадиях эволюции. Показано, что вращение влияет на уравнение состояния и приводит к неустойчивости невращающихся решений, что указывает на его фундаментальную роль в подобных сценариях. Можно ли, таким образом, разработать новые космологические модели, учитывающие влияние сверхтекучих сред и вращения для более точного описания наблюдаемой вселенной?
Космологический принцип: Основы и допущения
Современная космология базируется на космологической модели, постулирующей удивительную однородность Вселенной в пространстве и изотропность по направлениям. Это означает, что, в крупном масштабе, Вселенная выглядит одинаково, вне зависимости от того, где находится наблюдатель и в каком направлении он смотрит. Данное предположение, известное как космологический принцип, значительно упрощает математическое описание эволюции Вселенной, позволяя применять единые физические законы к любым её частям. Хотя наблюдаемые локальные структуры, такие как галактики и скопления галактик, демонстрируют неоднородность, в среднем, на масштабах сотен миллионов световых лет, Вселенная действительно соответствует этим требованиям однородности и изотропности, что подтверждается наблюдениями реликтового излучения и крупномасштабной структуры Вселенной. Именно это фундаментальное свойство позволяет строить математические модели, описывающие расширение Вселенной и её эволюцию во времени.
В основе современной космологической модели лежит тензор энергии-импульса, математический инструмент, описывающий распределение энергии и материи во Вселенной. Этот тензор, обозначаемый как $T_{\mu\nu}$, включает в себя плотность энергии, давление и поток импульса в каждой точке пространства-времени. Изучение этого тензора позволяет установить связь между распределением вещества и геометрией Вселенной, определяя её эволюцию. Например, доминирование различных компонентов, таких как темная энергия или темная материя, проявляется в структуре тензора, влияя на скорость расширения и формирование крупномасштабных структур. По сути, тензор энергии-импульса служит фундаментальным строительным блоком для уравнений Эйнштейна, описывающих гравитационное поле и определяющих динамику Вселенной.
Успех стандартной космологической модели во многом определяется уравнением состояния, которое устанавливает связь между давлением и плотностью различных компонентов Вселенной. Это уравнение, по сути, является ключом к пониманию того, как быстро расширяется пространство. Например, для идеального газа уравнение состояния имеет вид $p = k\rho$, где $p$ — давление, $\rho$ — плотность, а $k$ — константа. Однако для описания Вселенной используются более сложные уравнения, учитывающие влияние темной энергии и темной материи. В зависимости от соотношения между давлением и плотностью, различные компоненты могут либо ускорять, либо замедлять расширение. Точное определение уравнения состояния для этих загадочных субстанций остается одной из главных задач современной космологии, поскольку от этого напрямую зависит предсказание будущей судьбы Вселенной.
Нарушение симметрии: Анизотропное расширение и отклонения
Отклонения от полной изотропии и однородности в космологических моделях проявляются в виде анизотропного расширения, которое характеризуется наличием сдвига ($shear$) и вращения. Сдвиг описывает деформацию объема пространства, когда скорости расширения различаются в разных направлениях, приводя к изменению формы объектов. Вращение, в свою очередь, подразумевает наличие угловой скорости расширения, которая также варьируется в зависимости от направления. Эти эффекты не являются случайными флуктуациями, а представляют собой систематические отклонения от стандартной модели космологии, требующие для своего описания более сложных математических аппаратов и, возможно, пересмотра базовых предположений о природе пространства-времени.
Группа Литья, расширенная группой $SL(2,R)$, определяет симметрии пространства-времени в заданной точке, что оказывает влияние на развитие анизотропий. В классической общей теории относительности группа Литья описывает локальные преобразования Лоренца, сохраняющие метрический тензор. Расширение до $SL(2,R)$ позволяет учитывать дополнительные степени свободы, связанные с возможными деформациями и вращениями пространства-времени. Конкретно, элементы $SL(2,R)$ соответствуют локальным бустам и вращениям, которые могут приводить к анизотропному расширению Вселенной, то есть к различным скоростям расширения в разных направлениях. Анализ симметрий, задаваемых расширенной группой Литья, является ключевым для понимания происхождения и эволюции анизотропий в космологических моделях.
Анизотропные эффекты в космологических моделях математически описываются посредством расширений стандартной модели, одним из примеров которых является метрика Бианки I. Данная метрика, являясь частным случаем более общей метрики Бианки, представляет собой решение уравнений Эйнштейна в случае однородной и изотропной Вселенной с направленным расширением. Она характеризуется тензором метрики, который учитывает различную скорость расширения вдоль различных осей, в отличие от стандартной космологической модели Фридмана — Леметра — Робертсона — Уокера (FLRW), предполагающей одинаковую скорость расширения во всех направлениях. Математически, метрика Бианки I имеет вид $ds^2 = -dt^2 + a_1^2 dx^2 + a_2^2 dy^2 + a_3^2 dz^2$, где $a_i(t)$ — масштабные факторы, описывающие расширение или сжатие пространства вдоль соответствующих осей. Изучение метрики Бианки I позволяет исследовать космологические модели с анизотропным расширением и их влияние на формирование крупномасштабной структуры Вселенной.
Экзотические поля и новые космологии
Сдвигосимметричные скалярные поля ($\phi$) предоставляют теоретическую основу для моделирования сверхтекучих сред, где флуктуации поля могут описывать коллективные возбуждения, аналогичные фононам в твердом теле. Помимо этого, в космологических сценариях, наличие нескольких сдвигосимметричных полей может приводить к анизотропному расширению Вселенной. Это связано с тем, что различные поля могут обладать различными пространственными градиентами, создавая асимметрию в давлении и, следовательно, отклонение от изотропного расширения, характерного для стандартной космологической модели Фридмана — Леметра — Робертсона — Уокера (FLRW).
Поле Галилеона, являющееся специфическим типом скалярного поля, представляет собой теоретический механизм, способный нарушать предсказания теоремы об отсутствии волос (No-Hair Theorem) для чёрных дыр. Данная теорема утверждает, что чёрные дыры полностью характеризуются лишь массой, зарядом и угловым моментом. Поле Галилеона, благодаря своим нелинейным самодействиям, позволяет создавать чёрные дыры, обладающие дополнительными параметрами, отличными от указанных, что приводит к появлению «волос» и, следовательно, противоречит стандартной модели. Это обусловлено тем, что производные поля Галилеона входят в лагранжиан, что позволяет формировать решения, отличные от решений Керра-Ньюмана, описывающих чёрные дыры в общей теории относительности.
В рамках космологических моделей, включающих несколько сдвигово-симметричных скалярных полей, проведенное исследование показывает, что вращение проявляется как существенный динамический фактор. Это оказывает влияние на уравнение состояния, приводя к отклонениям от стандартных значений, характерных для радиационной эпохи. В частности, полученное уравнение состояния имеет параметр, равный $1/3$, в отличие от $1/2$ для излучения. Более того, асимптотическое поведение сдвигового напряжения стремится к постоянному значению $2/3$ при наличии вращения, что потенциально может быть связано с наблюдаемыми аномалиями в дипольном излучении реликтового излучения и требует дальнейшего изучения.
В рамках исследуемых космологических сценариев с использованием множественных скалярных полей, параметр уравнения состояния ($w$) был рассчитан и составил 1/3. Это значение существенно отличается от стандартного для излучения, где $w = 1/2$. Отклонение от стандартного значения указывает на модифицированное поведение энергетической плотности и давления в рассматриваемой модели, что потенциально может объяснить наблюдаемые аномалии и отличия от предсказаний стандартной космологической модели. Данный результат предполагает необходимость пересмотра стандартных предположений о составе Вселенной и динамике её расширения.
В рамках исследуемых космологических сценариев с участием нескольких скалярных полей, демонстрирующих сдвиговую симметрию, установлено, что асимптотическое поведение сдвига (shear) стремится к постоянному значению, равному 2/3, при наличии вращения. Данный результат получен на основе анализа уравнений, описывающих эволюцию метрики пространства-времени в присутствии вращательных компонент. Постоянное значение сдвига указывает на то, что деформация пространства-времени, вызванная вращением, стабилизируется со временем и не приводит к дальнейшему ускорению или замедлению деформации. Это отличает данную модель от стандартных космологических моделей, где сдвиг обычно изменяется во времени.
Исследование космологических сценариев с движущимися сверхтекучими средами, представленное в данной работе, подчеркивает возрастающую роль вращения в поздние времена. Это вращение, как показано, оказывает влияние на уравнение состояния и может приводить к неустойчивости невращающихся решений. В связи с этим вспоминается высказывание Сергея Соболева: «В науке, как и в жизни, нельзя предсказать все последствия своих действий». Действительно, анализ эволюции подобных систем требует применения численных методов и анализа устойчивости решений уравнений Эйнштейна, поскольку даже незначительные начальные условия могут привести к непредсказуемым последствиям в масштабах Вселенной. Игнорирование вращения, как показано в статье, может привести к неверным выводам о состоянии и эволюции сверхтекучей среды в расширяющейся Вселенной.
Куда же это всё ведёт?
Рассмотренные здесь модели, описывающие движение сверхтекучих сред во вращающейся Вселенной, не столько дают ответы, сколько обнажают глубокие вопросы. Представление о смещении симметрии как о ключе к космологическим сценариям, безусловно, элегантно, однако стабильность невращающихся решений, как показывает анализ, представляется скорее исключением, чем правилом. Это, разумеется, не приговор для подхода, но напоминание о том, что даже самые изящные математические конструкции могут оказаться хрупкими перед лицом динамической реальности.
Очевидным направлением дальнейших исследований является углубленный анализ влияния вращения на уравнение состояния. Игнорирование анизотропии, столь привычное в космологических моделях, может оказаться грубой аппроксимацией, особенно на поздних стадиях эволюции Вселенной. Вероятно, настоящая картина гораздо сложнее и требует более тонких инструментов, чем стандартный подход «мини-пространства». Каждая новая модель — это лишь свет, который не успел исчезнуть за горизонтом событий.
В конечном счёте, эта работа, как и любая другая в этой области, служит напоминанием о том, что космология — это не поиск окончательной истины, а постоянное приближение к ней. Попытка описать Вселенную с помощью математических моделей — это всегда акт веры, который может быть опровергнут первыми же данными. Чёрная дыра, в конце концов, — это не просто объект, это зеркало нашей гордости и заблуждений.
Оригинал статьи: https://arxiv.org/pdf/2511.17472.pdf
Связаться с автором: https://www.linkedin.com/in/avetisyan/
Смотрите также:
- Тёмная энергия: новый взгляд на расширение Вселенной
- Радиоастрономия на новом уровне: поиск темной энергии с помощью гигантских телескопов
- Отпечатки ранней Вселенной: как эпоха реионизации сужает рамки для космологических моделей
- Галактики после столкновений: новый вклад в рост звездной массы
- Углерод в спирали галактики: происхождение и эволюция
- Ударные волны и рождение звезд: новый взгляд на химию протозвездных потоков
2025-11-25 06:06