Гравитоны и дефекты: новое измерение голографической корреляции

Автор: Денис Аветисян

Исследование раскрывает особенности взаимодействия массивных гравитонов с топологическими дефектами в рамках голографической дуальности.

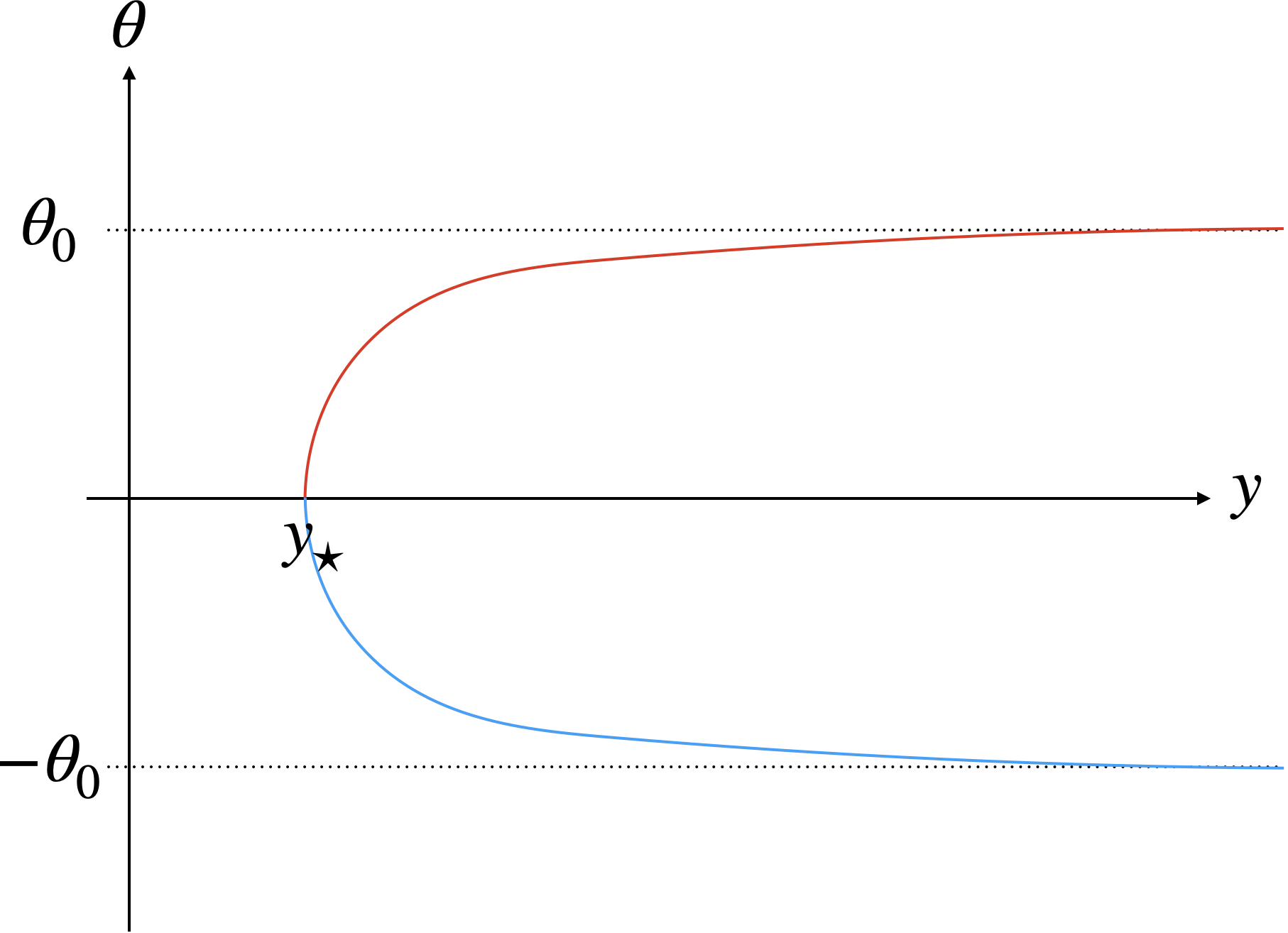
Геодезическая, зафиксированная в определенных точках, демонстрирует устойчивую структуру, способную адаптироваться к различным условиям и поддерживать форму благодаря внутренней силе натяжения.

В работе вычислены голографические корреляционные функции для гигантских гравитонов в фоне с монодромическими дефектами, используя калибровочную супергравитацию.

Несмотря на значительный прогресс в изучении корреляционных функций в конформной теории поля, влияние дефектов монодромии на динамику гигантских гравитонов оставалось недостаточно исследованным. В работе ‘Holographic Correlators of Giant Gravitons in Monodromy Defects’ предпринято вычисление голографических корреляторов для гигантских гравитонов в $\mathcal{N}=4$ SYM в присутствии таких дефектов, реализованных через пробные браны. Полученные результаты указывают на появление дополнительного вклада в двухточечную функцию, обусловленного геодезической, закрепленной на дефекте, что позволяет вычислить одноточечную функцию квадрата гигантского гравитона. Каким образом полученные результаты могут пролить свет на непертурбативную структуру конформных теорий поля с дефектами?

Сила Простоты: Голографическая Дуальность и N=4 ССМ

Теория N=4 суперсимметричной Янг-Миллса представляет собой исключительно плодородную площадку для изучения систем с сильным взаимодействием, однако аналитическое решение уравнений этой теории сопряжено со значительными трудностями. В отличие от слабых взаимодействий, где можно использовать методы теории возмущений, при сильных взаимодействиях стандартные подходы становятся неэффективными, а вычисления требуют новых, более сложных методов. Это связано с тем, что при сильных взаимодействиях возникают непертурбативные эффекты, которые невозможно точно описать с помощью стандартных методов теории поля. Именно эта сложность делает N=4 SYM столь интересным объектом для исследований, побуждая ученых искать альтернативные подходы к ее изучению, такие как голографическая дуальность, позволяющая перенести сложные вычисления в более доступную область классической гравитации.

Голографическая дуальность, в особенности соответствие AdS/CFT, представляет собой мощный инструмент для изучения сильновзаимодействующих систем. Оно позволяет установить связь между квантовой теорией поля, такой как N=4 суперсимметричная теория Янга-Миллса, и классической теорией гравитации в пространстве Анти-де Ситтера. По сути, это соответствие предполагает, что информация о квантовой теории, обитающей на ее границе, полностью закодирована в гравитационном поле, описывающем внутреннюю структуру пространства. Такой подход позволяет заменить сложные квантовые вычисления на более доступные классические расчеты в гравитации, открывая новые возможности для понимания непертурбативных аспектов N=4 SYM и других теорий, находящихся за пределами возможностей стандартных методов.

Данная дуальность позволяет исследовать явления в N=4 суперсимметричной теории Янга-Миллса посредством вычислений в 5-мерной калибровочной супергравитации. Использование гравитационного описания, классической теории, для анализа сильносвязанной квантовой теории открывает принципиально новые возможности для решения задач, недоступных прямым квантово-полевым методам. В частности, эта связь позволяет изучать непертурбативные аспекты N=4 SYM, то есть поведение системы при сильных взаимодействиях, где стандартные методы теории возмущений оказываются неэффективными. Вычисления в 5D калибровочной супергравитации, будучи классическими, предоставляют приближенные решения, которые могут быть использованы для понимания сложного поведения N=4 SYM в этом режиме, приближая исследователей к более полному пониманию фундаментальных свойств этой теории и связанных с ней явлений.

Дефекты, Геодезические и Гравитационный Дуал

Дефекты монодромии, представляющие собой нетривиальные граничные условия в N=4 ССМ (Суперсимметричной Теории Янга-Миллса), моделируются как поверхности коразмерности два в пятимерном фоне калибровочной СУГРА (Супергравитации). Это означает, что дефекты рассматриваются как объекты, имеющие две пространственные координаты меньше, чем пространство, в котором они находятся. В контексте дуальности AdS/CFT, это позволяет связать свойства дефектов в теории поля с геометрией пространства-времени в гравитационном дуале. Коразмерность два соответствует тому, что дефект локально изменяет геометрию пятимерного пространства, не влияя на все его измерения.

Ожидаемые значения операторов, заряженных относительно симметрии, связанной с дефектом, вычисляются посредством длин геодезических в гравитальном дуале. В рамках этой процедуры, геодезические, представляющие собой кратчайшие пути в искривленном пространстве-времени, вычисляются с учетом влияния дефекта на метрику. Длина такой геодезической напрямую соответствует значению одноточечной функции соответствующего оператора, позволяя установить количественную связь между геометрическими свойствами гравитационного дуала и квантово-полевыми свойствами теории N=4 SYM. В частности, отклонение длины геодезической от значения в отсутствии дефекта отражает вклад дефекта в корреляционные функции.

Одноточечная функция гигантского гравитона в дуальности AdS/CFT определяется длиной ‘заякоренных’ геодезических, начинающихся на дефектной поверхности. Геодезические, зафиксированные на дефекте, представляют собой кратчайшие пути в пространстве AdS, и их длина напрямую связана со значением одноточечной функции. Этот подход позволяет геометрически интерпретировать влияние дефекта на динамику гигантского гравитона, предоставляя конкретный способ вычисления его вакуумного среднего в теории N=4 SYM посредством решения геодезических уравнений в 5D пространстве Гауджед SUGRA. $\langle O \rangle \propto \text{length of anchored geodesic}$ .

Вычисление Корреляционных Функций с Заряженными Геодезическими

Для упрощения вычислений в рамках данной работы используется STU модель, представляющая собой усечение 5-мерной калибровочной супергравитации (Gauged SUGRA). Данное усечение позволяет снизить вычислительную сложность, сохраняя при этом ключевые характеристики, релевантные для описания гигантских гравитонов. STU модель характеризуется специфическим набором параметров и полей, определяющих геометрию пространства-времени, и позволяет эффективно исследовать корреляционные функции операторов в контексте голографической двойственности AdS/CFT. Выбор данной модели обусловлен ее способностью адекватно моделировать динамику гигантских гравитонов и корреляционные функции, что делает ее удобным инструментом для проведения аналитических и численных расчетов.

Для вычисления двухточечной функции гигантских гравитонов используется подход с «заряженными геодезическими» — геодезическими, движущимися в пространстве-времени с определенными зарядами. Этот метод обеспечивает голографическое представление корреляционной функции операторов. Полученные результаты показывают, что стандартный вклад в двухточечную функцию масштабируется как $e^{-2S_{os}}$ , и пропорционален $β^{0}$ , то есть не зависит от силы дефекта β. Это означает, что вклад стандартной геодезической в корреляционную функцию остается постоянным, вне зависимости от величины дефекта в рассматриваемой модели.

Сравнение стандартной ‘U-образной геодезической’ с модифицированными геодезическими вблизи дефекта демонстрирует влияние дефекта на корреляционную функцию. Вклад от ‘якорной геодезической’ масштабируется линейно с силой дефекта β, что приводит к одноточечной функции, пропорциональной $e^{-4mβ}$ . Это означает, что наличие дефекта вносит дополнительный вклад в корреляционную функцию, величина которого напрямую зависит от параметра β, характеризующего силу дефекта, и экспоненциально подавляется при увеличении $m$ . Полученный результат указывает на то, что дефект изменяет пространственную структуру корреляций операторов, внося поправку, пропорциональную силе дефекта.

Значение Результатов и Перспективы Дальнейших Исследований

Представленная работа предлагает мощный инструментарий для исследования влияния дефектов на корреляционные функции в сильносвязанных системах, предоставляя возможности, выходящие за рамки стандартных возмущающих вычислений. В отличие от традиционных подходов, часто ограниченных слабыми взаимодействиями, данная методика позволяет анализировать системы, где взаимодействия настолько сильны, что возмущающие ряды расходятся. Это особенно важно для понимания физики конденсированного состояния, таких как высокотемпературная сверхпроводимость и квантовые спиновые жидкости, где сильные корреляции играют ключевую роль. Благодаря разработанному фреймворку становится возможным детальное изучение того, как даже незначительные дефекты в структуре материала могут существенно изменять его квантовые свойства, открывая новые пути для управления и оптимизации функциональных материалов.

Использование голографического подхода позволяет рассматривать нелокальные эффекты, вносимые дефектом, с геометрической точки зрения. В рамках данной модели, квантовая запутанность, являющаяся фундаментальным свойством сильно взаимодействующих систем, проявляется как геометрическая связь в дополнительном измерении. Дефект, представляющий собой нарушение в структуре системы, отображается как искривление этого дополнительного пространства, напрямую влияя на степень запутанности между различными частями системы. Таким образом, возникает глубокая связь между геометрией этого искривленного пространства и характеристиками квантовой запутанности, позволяющая исследовать нелокальные корреляции, недоступные для анализа традиционными методами теории возмущений. Это открывает новые возможности для понимания свойств сильно коррелированных систем и изучения влияния дефектов на их квантовое поведение.

Дальнейшие исследования направлены на расширение применимости разработанного подхода к более сложным конфигурациям дефектов, включая анализ их влияния на динамику конфайнмента и другие непертурбативные явления. Ожидается, что изучение взаимодействия дефектов различной геометрии позволит получить новые сведения о механизмах, лежащих в основе формирования нелокальных эффектов в сильносвязанных системах. В частности, планируется исследовать, как конфигурация дефекта влияет на структуру корреляционных функций и, следовательно, на свойства квантовой запутанности в системе. Результаты этих исследований могут способствовать лучшему пониманию фазовых переходов и критических явлений, а также найти применение в разработке новых материалов с заданными свойствами.

Исследование, представленное в статье, демонстрирует изящную простоту в вычислении голографических корреляционных функций. Авторы, подобно хирургам, отсекают избыточные сложности, фокусируясь на ключевом вкладе геодезической, закрепленной у дефекта монодромии. Эта точность напоминает о словах Симоны де Бовуар: «Не существует ничего, кроме существования». Подобно тому, как философ стремилась к ясной истине, лишенной всего лишнего, данная работа подчеркивает фундаментальную роль геодезических в понимании взаимодействия гигантских гравитонов, выявляя основную структуру голографической дуальности AdS/CFT. Игнорирование второстепенного позволяет увидеть ясную картину взаимодействия в рамках данной модели.

Что дальше?

Представленные вычисления, хотя и демонстрируют конкретный вклад геодезической, закрепленной в дефекте, лишь намекают на сложность голографических корреляционных функций в присутствии монодромийных дефектов. Очевидно, что поиск универсального подхода, не зависящего от деталей выбранной супергравитационной модели, остаётся главной задачей. Стремление к изяществу требует отказа от излишних параметров и сосредоточения на фундаментальных принципах, определяющих поведение этих систем.

Необходимо учитывать, что полученный результат относится к конкретному типу гигантских гравитонов. Расширение анализа на другие классы операторов и рассмотрение более сложных конфигураций дефектов, включая их взаимодействие, представляется неизбежным шагом. Истинное понимание требует не просто получения ответов, но и осознания границ применимости полученных результатов.

В конечном счёте, совершенство этого направления исследований не в увеличении числа вычисленных корреляционных функций, а в исчезновении необходимости в их вычислении. Иными словами, цель состоит не в том, чтобы заполнить пробелы в знаниях, а в создании единой, непротиворечивой картины, объясняющей наблюдаемые явления. Лишь тогда можно будет утверждать, что задача, поставленная AdS/CFT корреспонденцией, действительно решена.

Оригинал статьи: https://arxiv.org/pdf/2601.10788.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-01-20 08:43