Автор: Денис Аветисян
Новое исследование показывает, как принцип масштабно-инвариантности в ньютоновской гравитации может приводить к спонтанному возникновению структур, таких как нити, и определять направление времени.
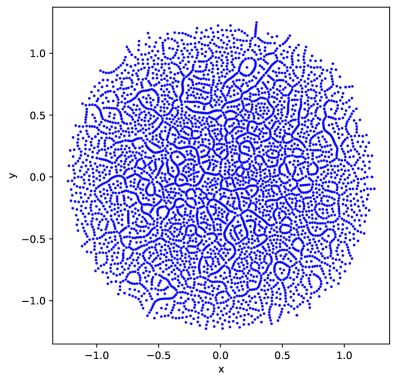
В работе исследуется связь между масштабно-инвариантностью, центральными конфигурациями и возникновением упорядоченных структур в ньютоновской гравитации.
Несмотря на фундаментальную роль, инвариантность относительно масштаба долгое время оставалась за пределами пристального внимания в физических исследованиях. В работе ‘Scale Invariance, Variety and Central Configurations’ предложен формализм, основанный на рассмотрении $N$-частичной задачи, где вводится величина — «вариативность» V, построенная из момента инерции центра масс и ньютоновского потенциала, позволяющая исследовать конфигурации, сохраняющие форму при гомотетическом расширении или сжатии. Показано, что критические точки этой функции соответствуют особым расположениям частиц, а небольшие отклонения от абсолютного минимума V приводят к спонтанному формированию нитей, петель и пустот, напоминающих космическую сеть. Может ли такой подход, основанный на реляционной динамике и инвариантности относительно масштаба, предложить новый взгляд на формирование космических структур и возникновение гравитационной стрелы времени?
За пределами абсолютных значений: Реляционная основа понимания
Традиционные подходы к задаче N тел, как правило, сосредотачиваются на абсолютных координатах каждого объекта, что приводит к упущению важных симметрий и упрощению картины гравитационного взаимодействия. Принятие абсолютных позиций в качестве отправной точки часто маскирует внутреннюю структуру системы, игнорируя тот факт, что физические законы должны быть инвариантны относительно изменений в системе координат. Это приводит к трудностям при моделировании сложных систем, где относительное расположение тел играет более важную роль, чем их абсолютные координаты. Например, при рассмотрении столкновений или взаимодействий между галактиками, важно понимать не столько, где они находятся в абсолютном пространстве, сколько как они движутся относительно друг друга. Учет лишь абсолютных позиций может привести к неточным результатам и упущению ключевых аспектов динамики системы, скрывая фундаментальные закономерности, определяющие ее эволюцию.
Вместо того чтобы рассматривать положение каждого тела в абсолютном пространстве, предлагается новый подход к решению N-задач о движении тел, фокусирующийся на отношениях между самими телами. Данная парадигма предполагает, что динамика системы определяется не абсолютными координатами, а расстояниями и относительными скоростями между составляющими её объектами. Такой сдвиг в перспективе позволяет избавиться от произвольных выборов начала координат и упростить математическое описание гравитационных взаимодействий. Вместо слежения за каждым телом как за отдельной сущностью, внимание концентрируется на том, как тела влияют друг на друга, что открывает путь к более элегантным и обобщенным решениям, менее зависимым от конкретных начальных условий и масштаба рассматриваемой системы. \frac{d}{dt} взаимного расположения тел становится ключевым параметром, определяющим эволюцию системы.
Перспектива, основанная на масштабно-инвариантности, открывает путь к более надежному и универсальному пониманию гравитационных систем. В отличие от традиционных подходов, которые фиксируются на абсолютных координатах и, следовательно, упускают из виду фундаментальные симметрии, данный подход подчеркивает, что поведение системы определяется исключительно отношениями между телами, а не их положением в абсолютном пространстве. Это означает, что законы гравитации могут быть применены к системам любого масштаба — от галактик до элементарных частиц — без необходимости введения дополнительных параметров или корректировок. N-тельные задачи, рассматриваемые с этой точки зрения, демонстрируют устойчивость к изменениям масштаба, что позволяет разрабатывать более общие модели и предсказывать поведение систем в широком диапазоне условий. Игнорирование абсолютных значений и фокусировка на относительных отношениях между телами приводит к упрощению уравнений и повышению точности прогнозов, особенно в сложных и динамичных системах.
Определение разнообразия: Масштабно-инвариантный дескриптор
Разнообразие, определяемое как отношение среднеквадратичной длины к средней гармонической длине, представляет собой шкало-инвариантную меру распределения частиц. Variety = \frac{RMS \ length}{Mean \ harmonic \ length} Среднеквадратичная длина рассчитывается как квадратный корень из суммы квадратов расстояний каждой частицы от центра масс системы, нормализованный на общее количество частиц. Средняя гармоническая длина вычисляется как обратное среднему арифметическому обратных расстояний от каждой частицы до центра масс. Использование этого отношения позволяет получить значение, не зависящее от общего размера системы, что обеспечивает возможность сравнения распределений частиц в системах различных масштабов.
Величина разнообразия, определяемая как отношение среднеквадратичной длины к средней гармонической длине, является инвариантной относительно общего размера системы. Это означает, что значение разнообразия не изменяется при масштабировании всей системы, позволяя проводить содержательное сравнение распределений частиц в системах, различающихся по своим абсолютным размерам. Фактически, Variety = \frac{RMS\ length}{Mean\ harmonic\ length} представляет собой безразмерную величину, что делает ее применимой для анализа систем с различными единицами измерения длины и гарантирует, что различия в значениях разнообразия отражают реальные различия в структуре распределения частиц, а не просто различия в масштабе.
Величина Variety, определяемая как отношение среднеквадратичной длины к средней гармонической длине, отражает баланс между расширением и концентрацией частиц в системе. Зависимость от обеих мер — среднеквадратичной и гармонической — позволяет оценить степень разброса частиц относительно центра и степень их уплотнения вокруг определенных точек. Этот баланс критически важен для понимания процессов формирования структуры, поскольку определяет, будет ли система стремиться к однородному распределению частиц или к образованию кластеров и неоднородностей. Variety = \frac{RMS \ length}{Mean \ harmonic \ length} Именно этот показатель позволяет количественно оценить вклад как расширения, так и концентрации в общую структуру системы, что необходимо для анализа различных физических и химических процессов.

Пространство форм и появление структуры
В рамках подхода «Пространство Форм» (Shape Space) используется понятие «Разнообразия» (Variety) для геометрической характеризации конфигураций частиц. Variety представляет собой меру отклонения конфигурации от однородного состояния и позволяет количественно оценить её сложность. Данный подход позволяет рассматривать конфигурации частиц не как набор координат в евклидовом пространстве, а как точки в абстрактном пространстве форм, где близость точек соответствует сходству конфигураций. Это позволяет применять методы дифференциальной геометрии для анализа стабильности и эволюции многочастичных систем, а также выявлять закономерности в формировании сложных структур. Ключевым преимуществом является возможность характеризации конфигураций независимо от абсолютного масштаба и ориентации системы.
В рамках используемой нами системы координат «Shape Space», конфигурации, известные как Центральные Конфигурации и Равномерные Конфигурации, соответствуют экстремальным значениям величины Variety V. Это означает, что данные конфигурации представляют собой точки максимума или минимума V, что, в свою очередь, указывает на их стабильность или соответствие состояниям с минимальной энергией. Иными словами, отклонение от этих конфигураций требует затрат энергии, что обеспечивает их устойчивость в системе. Подобное соответствие между экстремальными значениями Variety и энергетической стабильностью является ключевым для понимания формирования структур в моделируемых системах.
Наши симуляции продемонстрировали спонтанное формирование нитевидных структур при отклонениях от абсолютного минимума величины V всего в 1.5%. Данное поведение было подтверждено в двумерных симуляциях, включающих 5000 частиц, и в трехмерных симуляциях с 1000 частиц, что свидетельствует о робастности данного явления и его независимости от размерности моделируемой системы. Наблюдаемое спонтанное формирование структур указывает на то, что даже небольшие возмущения от состояния с минимальным V могут приводить к заметным изменениям в конфигурации частиц и формированию упорядоченных структур.
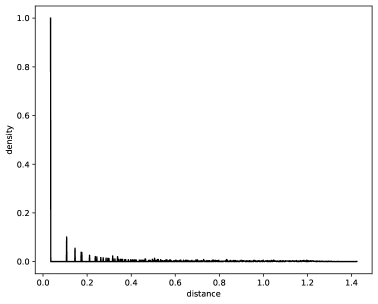
Разнообразие, точки Януса и стрела времени
Максимизация разнообразия является фундаментальным принципом, лежащим в основе формирования структур и возникновения сложных паттернов в различных системах. Исследования показывают, что стремление к увеличению вариативности, или разнообразия, способствует самоорганизации, приводя к появлению упорядоченных структур из хаоса. Этот процесс проявляется повсеместно — от формирования кристаллов и развития живых организмов до эволюции социальных систем и возникновения сложных технологических сетей. Чем больше возможностей для дифференциации и вариаций внутри системы, тем выше вероятность возникновения новых, более сложных и устойчивых структур, способных адаптироваться к изменяющимся условиям окружающей среды. Таким образом, разнообразие не просто является характеристикой сложных систем, но и является движущей силой их развития и эволюции.
Исследования показывают, что точки Януса, определяемые как минимумы момента инерции центра масс системы, тесно связаны с пиками разнообразия. Это означает, что в моменты, когда система достигает максимальной нестабильности и потенциала для изменений — как это проявляется в минимальном моменте инерции — наблюдается резкое увеличение числа возможных состояний и конфигураций. Такая корреляция указывает на ключевую роль точек Януса в процессах эволюции систем различного масштаба, от физических объектов до биологических организмов и даже социальных структур. Именно в этих точках происходит перераспределение энергии и информации, что способствует возникновению новых, более сложных форм организации и адаптации к изменяющимся условиям внешней среды. Таким образом, точки Януса можно рассматривать как критические моменты, определяющие траекторию развития системы и ее способность к самоорганизации.
Исследования показывают, что стремление системы к максимальному разнообразию — принципу, обозначаемому как Variety — тесно связано с ростом сложности и, что удивительно, с направленностью времени. Предполагается, что данное стремление к Variety выступает движущей силой, формирующей так называемую «гравитационную стрелу времени». В отличие от традиционных представлений о термодинамической стреле времени, основанной на энтропии, эта концепция предполагает, что сложность и разнообразие возникают не из хаоса, а как результат активного поиска системой состояний с максимальным Variety. Таким образом, увеличение сложности не является лишь следствием физических процессов, но и фундаментальной тенденцией, определяющей направление времени в данной системе, подобно гравитации, определяющей направление падения тел.
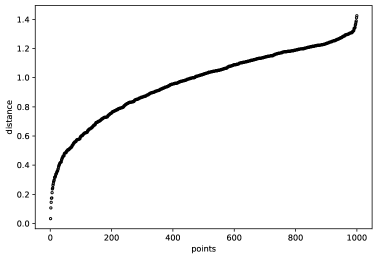
Исследование демонстрирует, что принцип масштабно-инвариантности в ньютоновской гравитации может быть не просто математическим удобством, а фундаментальным свойством, определяющим спонтанное возникновение структуры во Вселенной. Авторы предлагают рассматривать гравитацию не как силу, действующую в пространстве, а как свойство самого пространства, порождающее сложность. В этом контексте особенно примечательны слова Пьера Кюри: «Никогда не следует утверждать что-то абсолютно, поскольку абсолютных вещей в природе не существует». Именно эта осторожность в выводах и стремление к проверке гипотез прослеживаются в работе, где авторы, опираясь на математический формализм, предлагают механизм возникновения нитевидных структур и, как следствие, направления времени, без привлечения внешних сил или предположений.
Что дальше?
Предложенный подход, рассматривающий масштабную инвариантность как основополагающий принцип ньютоновской гравитации, не столько решает проблему возникновения структуры и “стрелы времени”, сколько переносит вопрос в иную плоскость. Вместо поиска внешних сил или начальных условий, анализ фокусируется на внутренних свойствах самой гравитационной динамики. Однако, стоит помнить: модель — это не зеркало мира, а зеркало аналитика. Представленные центральные конфигурации и нитевидные структуры — лишь один из возможных вариантов реализации этой динамики, и вопрос о критериях значимости, позволяющих отделить устойчивые образования от случайных флуктуаций, остается открытым.
Дальнейшие исследования, вероятно, потребуют более глубокого изучения пространства форм и его связи с вариацией нормализованного ньютоновского потенциала. Особый интерес представляет вопрос о влиянии начальных возмущений на эволюцию системы и о возможности возникновения самоподдерживающихся структур, устойчивых к внешним воздействиям. Следует также учитывать, что предложенный подход, будучи элегантным с теоретической точки зрения, нуждается в эмпирической проверке, пусть даже в рамках численных симуляций и лабораторных экспериментов с гравитационными аналогами.
В конечном итоге, ценность данной работы заключается не столько в окончательном ответе, сколько в постановке новых вопросов. Истина, как известно, рождается из последовательности проверок, ошибок и сомнений. И если предложенный подход окажется бесплодным, это лишь подтвердит, что поиск фундаментальных принципов, определяющих эволюцию Вселенной, — это бесконечный процесс.
Оригинал статьи: https://arxiv.org/pdf/2602.11225.pdf
Связаться с автором: https://www.linkedin.com/in/avetisyan/
Смотрите также:
- Галактика как ключ к пониманию Вселенной
- Тёмная энергия: новые сигналы из глубин Вселенной
- За гранью Стандартной модели: новые ограничения на взаимодействия нейтрино
- Карты неба: Новый взгляд на крупномасштабную структуру Вселенной
- Космологический парадокс: что не так с расширением Вселенной?
- Разгадка Напряженности Хаббла: Новая Модель Термического Вакуума
- Магнитные поля и рождение звезд: как устроена связь?
- Тёмная материя в шаровом скоплении Омега Центавра: новый взгляд из радиодиапазона
- Эхо Большого Взрыва: Поиск Отпечатков Ранней Вселенной в Галактиках
- Радиоэхо столкновений: активные ядра галактик в слиящихся группах
2026-02-14 02:59