Автор: Денис Аветисян
Исследование поведения вакуумных решений в $f(G, B)$ гравитации открывает возможности для более глубокого понимания структуры пространства-времени.
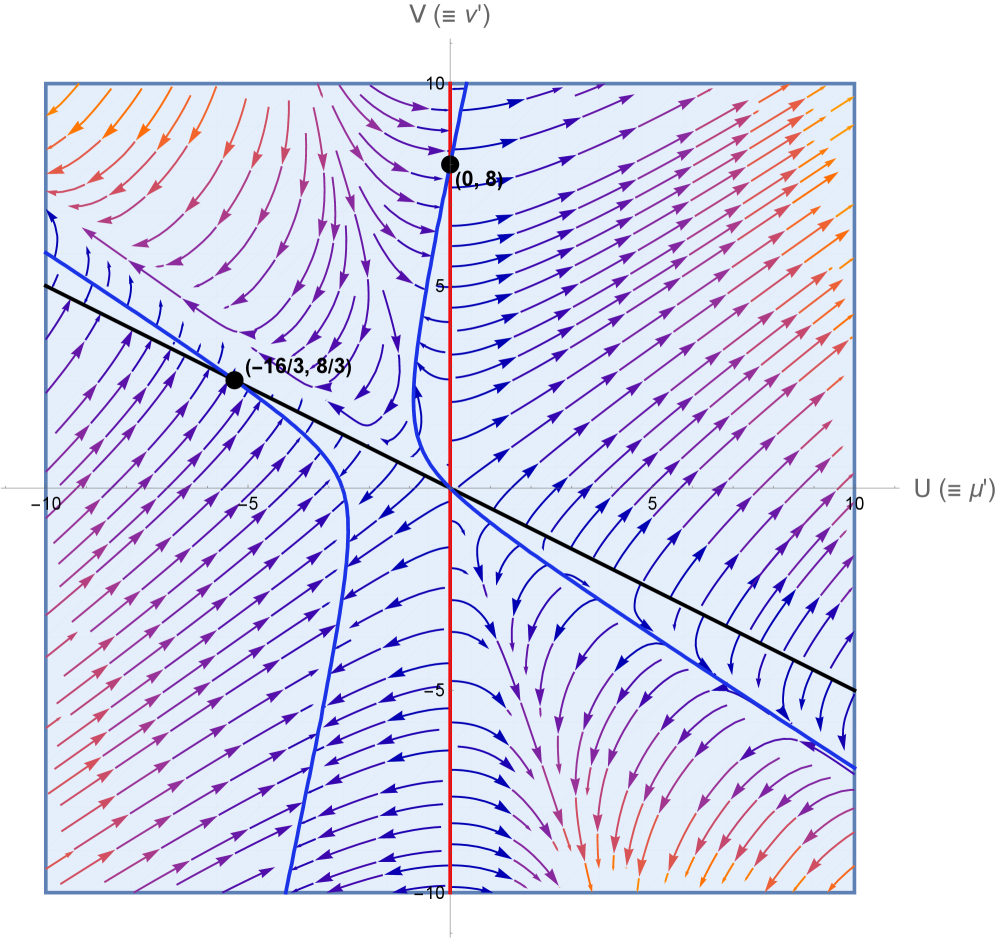
В статье представлен динамический анализ решений в $f(G, B)$ гравитации, фокусирующийся на квадратичной форме и позволяющий установить связи между метрическими функциями.
Традиционные модели звездной эволюции сталкиваются с трудностями при описании гравитационных взаимодействий, выходящих за рамки общей теории относительности. В работе ‘Dynamical systems approach to stellar modelling in $f(G, B)$ gravity’ предпринято исследование модифицированной теории гравитации f(G, B), в которой риччи-скаляр расщепляется на объемную и поверхностную компоненты. Получены два вакуумных решения, а анализ динамических систем позволил выявить устойчивые кривые, описывающие поведение метрических функций и направляющие построение точных решений. Каким образом дальнейшее развитие анализа динамических систем может способствовать углублению нашего понимания структуры и эволюции звезд в модифицированных теориях гравитации?
За пределами Эйнштейна: Ограничения Стандартной Гравитации
Несмотря на выдающийся успех теории гравитации Эйнштейна в описании множества явлений, она предсказывает возникновение сингулярностей — точек, где физические величины становятся бесконечными, а само пространство-время перестает быть гладким — в экстремальных условиях, таких как внутри черных дыр или в момент Большого взрыва. Эти сингулярности, математически выраженные через R_{abcd} тензор Римана и его скалярный аналог, указывают на принципиальные ограничения применимости общей теории относительности в этих областях. По сути, предсказание сингулярностей говорит о том, что теория «ломается», переставая давать физически осмысленные результаты, и требует разработки более полной теории гравитации, способной описывать поведение материи и энергии в условиях чрезвычайно сильных гравитационных полей и, возможно, учитывающей квантовые эффекты.
Сингулярности, возникающие в рамках общей теории относительности, представляют собой точки, где гравитационное поле становится бесконечно сильным, а сама геометрия пространства-времени теряет смысл. Эти сингулярности напрямую связаны с понятием кривизны пространства-времени, которое количественно оценивается с помощью скаляра Кретчманна R_{abcd}R^{abcd}. Высокие значения этого скаляра указывают на экстремальные условия, в которых предсказания теории становятся ненадежными, что свидетельствует о ее неполноте. Появление сингулярностей, например, в центрах черных дыр или в начальный момент Большого взрыва, бросает вызов фундаментальным представлениям о природе пространства и времени, требуя поиска новых физических теорий, способных описать гравитацию в этих экстремальных режимах и избежать предсказания бесконечностей.
Для преодоления ограничений общей теории относительности, особенно в экстремальных гравитационных полях, исследователи обращаются к модификациям этой теории, учитывающим квантовые эффекты. В областях, где гравитация становится чрезвычайно сильной, например, внутри черных дыр или в начальные моменты Большого взрыва, классическая общая теория относительности предсказывает сингулярности — точки, где плотность и кривизна пространства-времени становятся бесконечными. Квантовая гравитация, область, стремящаяся объединить принципы квантовой механики и общей теории относительности, предлагает потенциальные решения, вводя квантовые поправки к гравитационному полю. Эти поправки могут «сгладить» сингулярности, заменяя их областями высокой, но конечной плотности, и позволяя описать физику в этих экстремальных условиях. Активные исследования в этой области включают в себя теории струн, петлевую квантовую гравитацию и другие подходы, направленные на разработку последовательной теории квантовой гравитации, способной объяснить поведение пространства-времени на самых малых масштабах и в самых сильных гравитационных полях.
Модификация Гравитации: Теория f(G,B)
Один из перспективных подходов к модификации гравитации заключается в изменении действия (action) в общей теории относительности. Это приводит к появлению теорий, таких как f(G) гравитация, в которой действие является функцией скалярной кривизны G. Дальнейшим развитием является f(G,B) гравитация, представляющая собой расширение, включающее инвариант Гаусса-Бонне B в функциональную форму действия. Модификация действия позволяет исследовать альтернативные гравитационные модели, потенциально решающие проблемы стандартной общей теории относительности и предлагающие более полное описание гравитационных взаимодействий.
Теория `f(G,B) гравитации` представляет собой расширение стандартной гравитации, включающее в себя инвариант Гаусса-Бонне G и пограничный член B в действие Эйнштейна-Гильберта. Инвариант Гаусса-Бонне является топологической величиной, характеризующей кривизну пространства-времени, и добавляется для модификации гравитационных уравнений высшего порядка. Пограничный член необходим для корректного определения уравнений движения и обеспечения корректного поведения теории вблизи границ пространства-времени, а также для устранения артефактов, возникающих при варьировании пограничных условий. Включение обоих членов позволяет создавать модели, которые могут решать проблемы, связанные с сингулярностями и неполнотой общей теории относительности.
Целью построения теории f(G,B) является создание модели гравитации, свободной от сингулярностей, возникающих в классической общей теории относительности. Подбор функциональной формы f(G,B), учитывающей инвариант Гаусса-Бонне G и пограничный член B, позволяет модифицировать уравнения Эйнштейна и устранить точки, в которых плотность энергии и кривизна пространства-времени становятся бесконечными. Такой подход предполагает, что гравитация может быть более сложной, чем предсказано общей теорией относительности, и позволяет описать физические явления, требующие учета квантовых эффектов или экстремальных гравитационных условий, например, вблизи черных дыр или в ранней Вселенной.
Вакуумные Решения и Динамические Системы
Поиск вакуумных решений уравнений поля `f(G,B)` гравитации является фундаментальным для понимания космологических последствий данной теории. Вакуумные решения представляют собой конфигурации пространства-времени, свободные от материи и излучения, и служат базовым фоном для изучения эволюции Вселенной. Анализ этих решений позволяет установить связь между параметрами теории `f(G,B)` и наблюдаемыми космологическими величинами, такими как темп расширения Вселенной, наличие темной энергии и темной материи. Нахождение точных вакуумных решений, удовлетворяющих физически реалистичным условиям, является сложной математической задачей, но необходимым шагом для построения космологических моделей на основе `f(G,B)` гравитации. В частности, изучение поведения решений вблизи сингулярностей и при больших временах позволяет оценить стабильность и пригодность модели для описания ранней и поздней Вселенной.
Поиск вакуумных решений в гравитации f(G,B) напрямую зависит от свойств тензора Риччи R_{\mu\nu}. Физическая реалистичность этих решений требует выполнения определенных условий, ключевым из которых является асимптотическая плоскостность — то есть, гравитационное поле должно стремиться к нулю на больших расстояниях. Асимптотическая плоскостность гарантирует, что решение описывает изолированный гравитационный объект и соответствует наблюдаемым космологическим данным, исключая решения, представляющие собой нефизические сингулярности или бесконечные потоки энергии. Несоблюдение этого условия делает решение математически допустимым, но не имеющим физической интерпретации.
В рамках исследования гравитации f(G,B) были получены два различных вакуумных решения уравнений поля. Первое решение характеризуется плоскими пространственными сечениями, в то время как второе демонстрирует сингулярность кривизны. Для анализа динамического поведения этих решений был применен метод анализа фазового пространства. Данный подход позволил выявить точки равновесия — фиксированные точки — и исследовать их устойчивость, что необходимо для определения долгосрочного поведения соответствующих космологических моделей и оценки физической состоятельности полученных решений. \frac{d\phi}{dt} = f(\phi)
Стабильность и Поиск Шкальной Инвариантности
Стабильность вакуумных решений напрямую связана с динамикой лежащей в основе автономной системы, определяющей их эволюцию. Исследования показывают, что поведение этих решений не является случайным, а подчиняется строгим математическим правилам, заложенным в структуру системы. Любые отклонения от равновесия, возникающие в вакууме, не приводят к полному разрушению, а, напротив, затухают или преобразуются в новые, стабильные конфигурации, что свидетельствует о внутренней устойчивости системы. Понимание этой взаимосвязи позволяет предсказывать поведение вакуума в различных условиях и выявлять факторы, влияющие на его стабильность, что имеет ключевое значение для теоретической физики и космологии. Фактически, анализ автономной системы позволяет рассматривать вакуум не как статичное состояние, а как динамическую сущность, находящуюся в постоянном, но контролируемом изменении.
Исследование масштабно-инвариантности в рассматриваемой системе представляет собой мощный инструмент для оценки её устойчивости и прогностической способности. В рамках данной работы было показано, что при определённых условиях, свойства системы остаются неизменными при изменении масштаба координат, что указывает на фундаментальную симметрию. Это позволяет не только упростить анализ сложных решений, но и предсказывать поведение системы в различных условиях, экстраполируя результаты, полученные для одного масштаба, на другие. Обнаруженная масштабно-инвариантность предполагает, что система способна поддерживать стабильность даже при значительных возмущениях, что особенно важно при моделировании физических процессов и разработке предсказательных моделей. Такой подход позволяет выявить универсальные закономерности, не зависящие от конкретных параметров системы, и повысить точность долгосрочных прогнозов.
Анализ системы выявил не отдельные точки равновесия, а целые кривые, что свидетельствует о существенной симметрии в её решениях. Вместо дискретных состояний, система демонстрирует непрерывный спектр стабильных конфигураций, что существенно расширяет возможности предсказания её поведения. При этом, обнаружена одна вакуумная конфигурация, характеризующаяся неустранимой сингулярностью кривизны. Данная сингулярность не поддается устранению посредством известных преобразований координат, что указывает на фундаментальную особенность данной конфигурации и требует дальнейшего изучения для понимания её физических последствий и потенциальной роли в эволюции системы. R_{\mu\nu} = 0 описывает геометрию пространства-времени, однако, для указанной конфигурации, данное уравнение не обеспечивает гладкость решения.
Представленное исследование, посвященное анализу решений в $f(G, B)$ гравитации, демонстрирует важность последовательного подхода к построению моделей. Авторы, исследуя поведение метрических функций в фазовом пространстве, стремятся не к установлению абсолютной истины, а к выявлению закономерностей и ограничений, накладываемых конкретной моделью гравитации. Как отмечал Марк Аврелий: «Всё, что мы видим, преходяще. Ибо не только изменение, но и прекращение всего есть часть потока Вселенной». Эта мысль созвучна методологии, применяемой в работе: поиск устойчивых решений и понимание пределов их применимости, признание того, что любая модель — лишь приближение к сложной реальности, а не её полное отражение. Изучение вакуумных решений и фазового пространства позволяет выявить не просто математические конструкции, а потенциальные характеристики геометрии пространства-времени, приближая нас к более глубокому пониманию Вселенной, даже если это понимание всегда будет неполным.
Что дальше?
Представленная работа, исследующая чисто квадратичную форму гравитации $f(G, B)$, выявляет, как обычно, не столько ответы, сколько новые, более изящные способы задать вопросы. Обнаружение двух вакуумных решений — это, конечно, забавно, но настоящая ценность заключается в применении анализа динамических систем. Данные не говорят о подобии метрических функций — их заставляют говорить. Впрочем, и этого достаточно, чтобы наметить пути для построения точных решений, если, разумеется, кто-то готов потратить время на проверку этих самых решений, а не на очередную трехмерную визуализацию «трендов».
Очевидное ограничение — рассмотрение лишь одного частного случая квадратичной формы. Чем больше визуализация — тем меньше проверка гипотез. Расширение на более общие функциональные зависимости, безусловно, потребует вычислительных усилий, но, возможно, и откроет новые, неожиданные ветви в пространстве решений. Более того, исследование стабильности полученных вакуумных решений и их поведения вблизи сингулярностей представляется задачей, требующей пристального внимания. Не стоит забывать и о космологических аспектах — как модифицированная гравитация $f(G, B)$ влияет на раннюю Вселенную и темную энергию?
В конечном итоге, данная работа — это лишь один шаг на пути к пониманию гравитации. Истина не рождается из одной модели, а вырастает из последовательности проверок, ошибок и сомнений. Остается надеяться, что последующие исследования будут столь же строги к собственным предположениям, как и к данным.
Оригинал статьи: https://arxiv.org/pdf/2602.11297.pdf
Связаться с автором: https://www.linkedin.com/in/avetisyan/
Смотрите также:
- Галактика как ключ к пониманию Вселенной
- Тёмная энергия: новые сигналы из глубин Вселенной
- За гранью Стандартной модели: новые ограничения на взаимодействия нейтрино
- Карты неба: Новый взгляд на крупномасштабную структуру Вселенной
- Космологический парадокс: что не так с расширением Вселенной?
- Разгадка Напряженности Хаббла: Новая Модель Термического Вакуума
- Радиоэхо столкновений: активные ядра галактик в слиящихся группах
- Космические нити рождения звёзд: обнаружены структуры в плотных облаках
- Танцующие тени: вращение экзотических компактных объектов
- Вселенная в фокусе: Новый взгляд на постоянную Хаббла
2026-02-15 05:49