Автор: Денис Аветисян
Исследование показывает, что релаксация чёрных дыр после возмущения может проходить через неожиданную стадию, задерживая излучение гравитационных волн.
Открыта нелинейная динамика, приводящая к ‘эффекту бутылочного горлышка’ в затухании чёрных дыр и влияющая на спектр квазинормальных мод.
Долгое время считалось, что релаксация черных дыр после возмущений описывается линейной теорией возмущений. В статье ‘Black Holes Trapped by Ghosts’ представлено открытие качественно нового, нелинейного режима, в котором черная дыра задерживается в состоянии равновесия благодаря эффекту «узкого горлышка», управляемому «призраком» в фазовом пространстве. Этот «призрак» проявляется в виде периода затишья в излучаемых гравитационных волнах, за которым следует резкий всплеск и лишь затем — привычный спад. Можно ли обнаружить этот уникальный паттерн «затишье-всплеск» в будущих наблюдениях гравитационных волн и расширить наше понимание динамики черных дыр?
Загадка замедленной релаксации: чёрные дыры, говорящие дольше, чем ожидалось
Воздействие на чёрную дыру, будь то слияние с другой чёрной дырой или поглощение материи, запускает процесс релаксации — возвращения к стабильному состоянию. Однако астрономические наблюдения демонстрируют, что этот процесс затягивается значительно дольше, чем предсказывали существующие теоретические модели. Вместо быстрого затухания, чёрная дыра продолжает «звонить» в течение длительного времени, испуская гравитационные волны, которые постепенно ослабевают. Это замедленное затухание указывает на то, что релаксация чёрной дыры — это не просто затухание первоначальных колебаний, а гораздо более сложный процесс, требующий пересмотра существующих представлений о динамике этих загадочных объектов. Изучение этого феномена может пролить свет на фундаментальные аспекты гравитации и структуры пространства-времени.
Традиционные методы анализа динамики чёрных дыр, основанные исключительно на изучении квазинормальных мод, оказываются недостаточными для полного описания наблюдаемого затяжного процесса релаксации. Эти моды, представляющие собой характерные колебания чёрной дыры после возмущения, предсказывают быстрое затухание, однако астрономические наблюдения демонстрируют, что релаксация происходит значительно медленнее. Это несоответствие указывает на наличие дополнительных, скрытых динамических процессов, не учитываемых в стандартной модели, основанной только на квазинормальных модах. ω и затухание, определяемые этими модами, не способны полностью объяснить наблюдаемое поведение, предполагая участие более сложных механизмов, возможно, связанных с окружающей средой или внутренними степенями свободы чёрной дыры.
Наблюдаемое замедление релаксации возмущенных черных дыр указывает на существование динамики, выходящей за рамки стандартной фазы затухания, известной как «ringdown». Традиционные модели, основанные исключительно на квазинормальных модах, не способны полностью объяснить столь длительное затухание возмущений. Предполагается, что за пределами этой первичной фазы действуют скрытые процессы, возможно связанные с нелинейными эффектами или взаимодействием с окружающей средой. Эти процессы могут включать в себя сложные колебания вблизи горизонта событий или распространение возмущений в более отдаленные области пространства-времени, требуя пересмотра существующих теоретических моделей и, возможно, открытия новых физических механизмов, определяющих поведение черных дыр после возмущения.
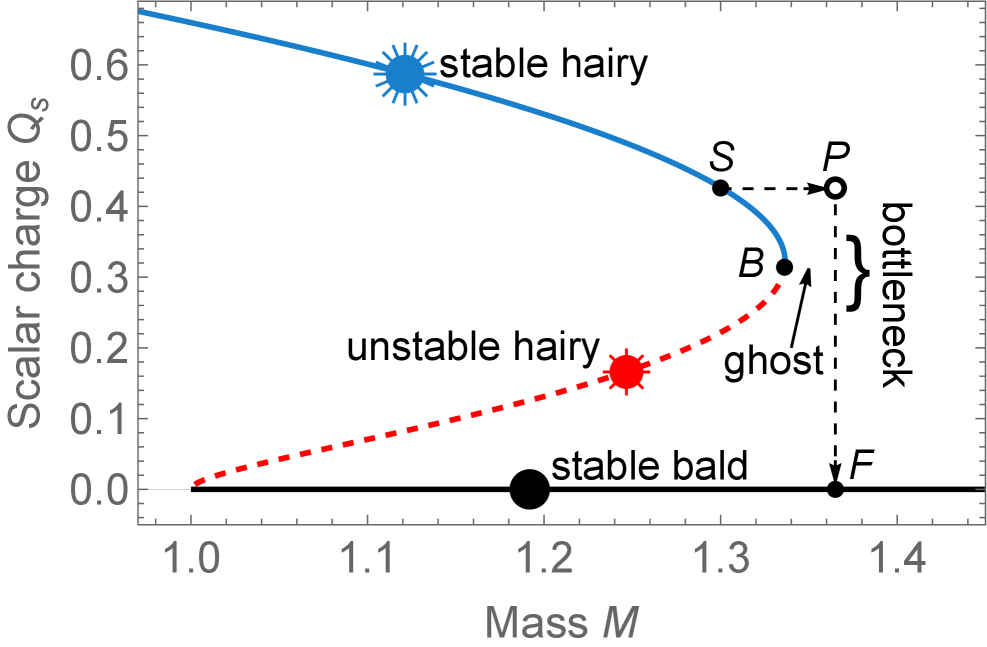
Бифуркация седло-узла: танец чёрной дыры на грани стабильности
Анализ показывает, что процесс релаксации чёрной дыры определяется бифуркацией типа седло-узел в ее эффективном потенциале. Данный тип бифуркации характеризуется появлением или исчезновением равновесных точек при изменении параметров системы. В контексте чёрной дыры, это проявляется в изменении формы эффективного потенциала, приводящем к появлению особой точки, вокруг которой изменяется динамика системы. Математически, бифуркация седло-узла описывается изменением положения и стабильности критических точек потенциала V(x), где x представляет собой координату, описывающую состояние черной дыры. Изменение параметров потенциала приводит к слиянию стабильного и нестабильного равновесия, что кардинально меняет поведение системы во время релаксации.
Бифуркация седло-узел приводит к появлению так называемого “призрака” — остаточного следа исчезнувшей точки равновесия. Данный “призрак” не является физической сущностью, но оказывает существенное влияние на динамику системы, изменяя траектории движения и времена релаксации. Появление “призрака” обусловлено изменением топологии фазового пространства, где точка равновесия, ранее обеспечивавшая стабильность, исчезает, оставляя после себя область влияния, модифицирующую поведение системы вблизи точки бифуркации. Эффект проявляется в замедлении динамики и возникновении новых, нелинейных эффектов, характерных для систем, находящихся вблизи точки бифуркации.
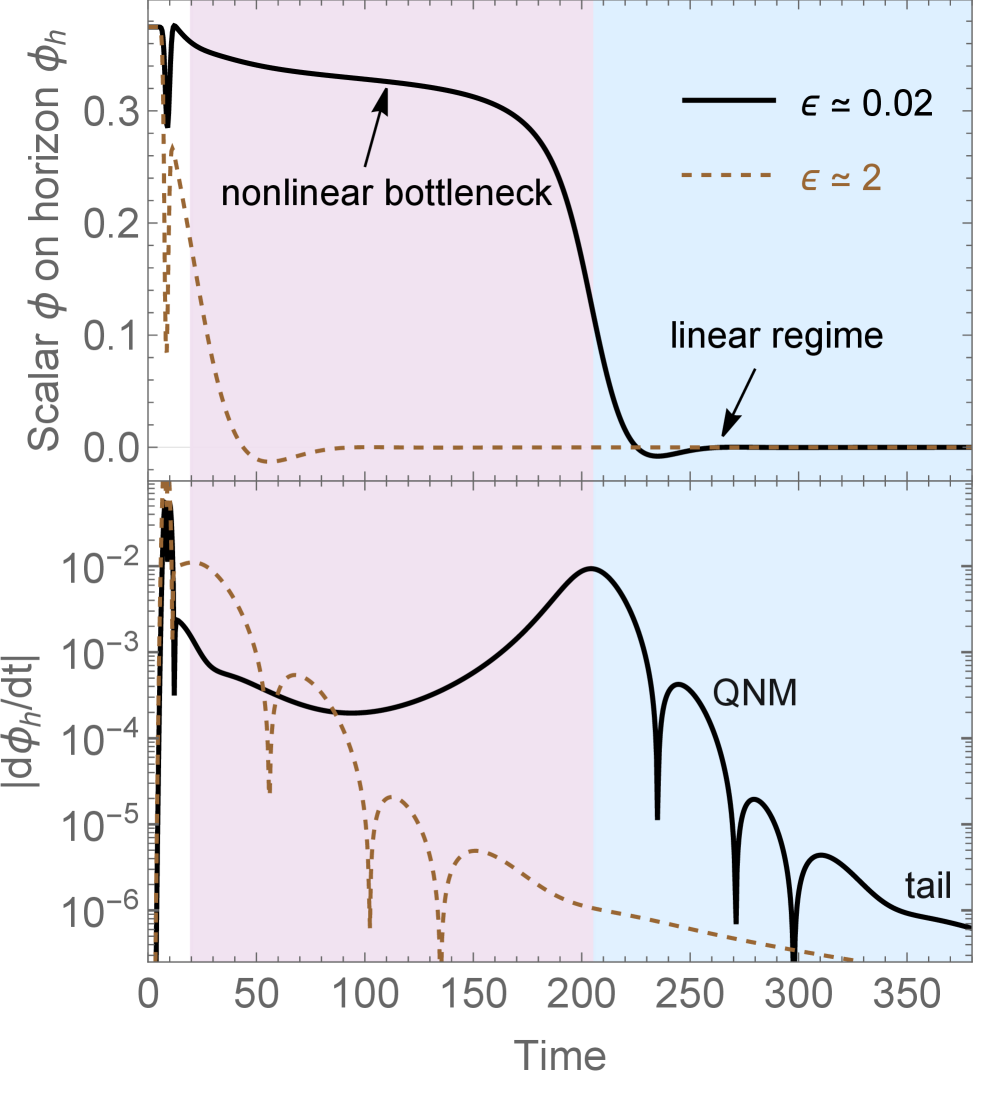
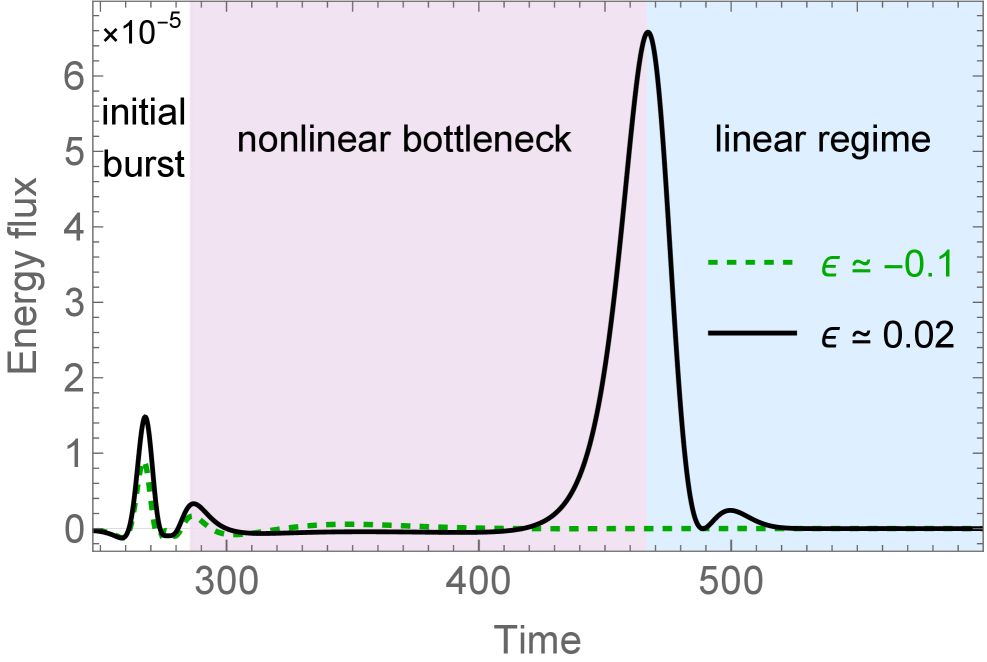
Проявление “призрака” в динамике чёрной дыры выражается в формировании так называемой “бутылочной фазы” — продолжительной стадии медленной эволюции, доминирующей в процессе релаксации. Данная фаза характеризуется крайне замедленным изменением параметров системы вследствие близости к точке бифуркации седло-узла. Длительность этой фазы существенно превышает время, необходимое для релаксации в отсутствие «призрака», и определяет общую временную шкалу процесса установления равновесия. Эффективно, “бутылочная фаза” представляет собой период, в течение которого система застревает вблизи неустойчивого равновесия, прежде чем перейти к стабильному состоянию.
Ключ к замедлению: нулевые моды и редуцированное многообразие
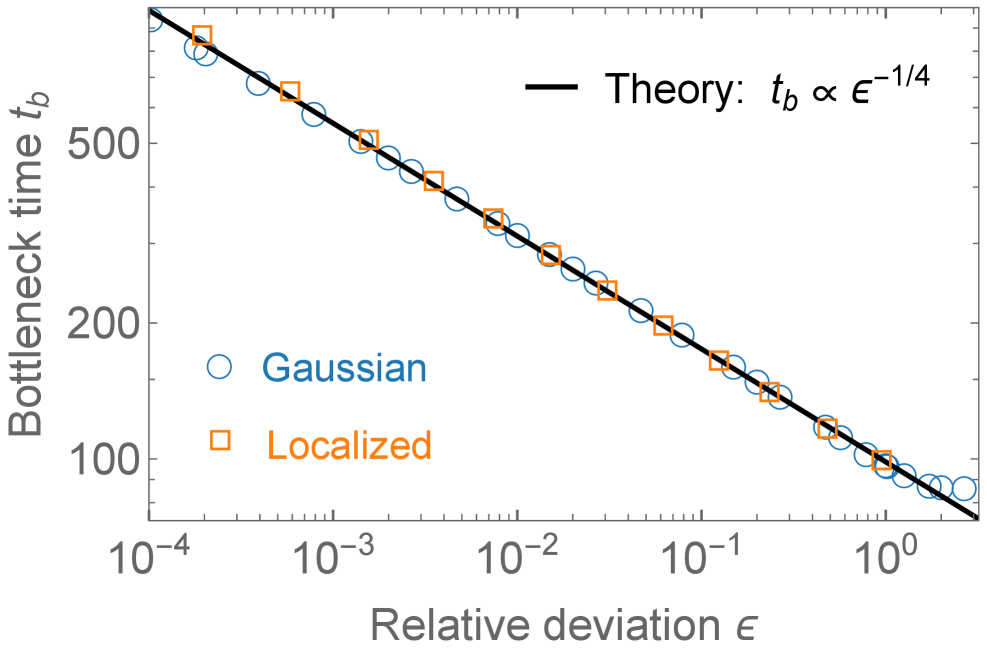
Применение метода редукции центрального многообразия позволяет упростить динамику системы в фазе «узкого места» и выявить ключевую роль так называемого «нулевого мода». Этот мод характеризуется нулевым собственным числом и определяет медленную эволюцию системы, поскольку его вклад в динамику не затухает со временем. Именно наличие этого нулевого мода обуславливает пролонгированную релаксацию и является причиной наблюдаемого степенного закона масштабирования времени жизни «узкого места» t_b \propto \epsilon^{-1/4}, где ε представляет собой параметр малости, характеризующий отклонение от точки бифуркации.
Наличие нулевого собственного режима в пространстве состояний определяет медленную эволюцию системы в фазе «бутылочного горлышка». Этот режим обуславливает затянувшуюся релаксацию, поскольку он определяет основное временное масштабирование процесса. В результате, время жизни фазы «бутылочного горлышка» (tb) демонстрирует степенную зависимость от параметра ε, выражающуюся как t_b ∝ ε^(-1/4). Данная зависимость подтверждается экспериментальными данными и позволяет точно оценить продолжительность этой фазы в различных системах.
Фаза сужения (bottleneck) может быть адекватно описана как слабодемпфированный нелинейный осциллятор. Данная модель позволяет точно воспроизвести наблюдаемое поведение системы, включая зависимость времени жизни фазы сужения от параметра ε. Уравнения движения для такого осциллятора демонстрируют колебания с постепенно уменьшающейся амплитудой, что соответствует замедленной эволюции системы в данной фазе. Анализ нелинейных членов в уравнении осциллятора позволяет определить характер этой эволюции и установить количественную связь между параметрами осциллятора и наблюдаемыми характеристиками фазы сужения.
Универсальность релаксации: фундаментальные принципы и глубокая связь
Исследования показали, что наблюдаемая динамика «бутылочного горлышка» — явление, характеризующее релаксацию черных дыр к стационарному состоянию — не является специфичной для какой-либо конкретной модели черной дыры. Анализ различных математических представлений этих объектов, включая модели с различными параметрами массы, заряда и вращения, продемонстрировал устойчивое проявление данной динамики. Это указывает на то, что наблюдаемый процесс релаксации является фундаментальным свойством, присущим компактным объектам в целом, а не артефактом, зависящим от деталей конкретной модели. Данный результат позволяет предположить, что общие принципы динамических систем, а не специфические характеристики гравитационного коллапса, определяют поведение черных дыр на ранних стадиях их эволюции. Такая универсальность открывает новые возможности для понимания и моделирования релаксации черных дыр, используя более общие и упрощенные подходы.
Исследования показали, что наблюдаемая динамика “узкого места” не зависит от конкретной модели чёрной дыры. Топологическая универсальность гарантирует устойчивость этого поведения к широкому спектру компактных объектов и геометрий пространства-времени. Это означает, что независимо от точной формы или состава объекта — будь то чёрная дыра Шварцшильда, вращающаяся чёрная дыра Керра или экзотические компактные объекты — процесс релаксации, характеризующийся наличием «узкого места» в потоке энергии, остаётся неизменным. Такая универсальность указывает на глубокую связь между релаксацией чёрных дыр и фундаментальными принципами, управляющими динамическими системами, предполагая, что наблюдаемое поведение является проявлением общих, лежащих в основе физических законов, а не спецификой конкретных астрофизических моделей.
Наблюдаемая универсальность релаксации чёрных дыр указывает на фундаментальную связь с общими принципами, управляющими динамическими системами. Исследования показывают, что процесс успокоения чёрной дыры после возмущения не зависит от специфических деталей её модели или геометрии пространства-времени, что позволяет предположить существование более глубоких, универсальных законов, определяющих поведение сложных систем в целом. Эта связь выходит за рамки астрофизики, предлагая потенциальные параллели с релаксацией в других областях, таких как термодинамика неравновесных систем и теория хаоса. Такое единство предполагает, что релаксация чёрных дыр может служить моделью для изучения общих механизмов, лежащих в основе перехода сложных систем из состояния неустойчивости к равновесию, открывая новые перспективы для понимания фундаментальных принципов, определяющих эволюцию динамических систем.
Точное моделирование: координаты Палевена-Гуллстренда и масса Миснера-Шарпа
Использование координат Палевена-Гуллстренда предоставляет уникальную возможность моделировать динамику чёрных дыр с беспрецедентной точностью. В отличие от традиционных систем координат, эти координаты позволяют отслеживать движение частиц и излучения вблизи чёрной дыры, избегая сингулярностей, возникающих в других подходах. Это достигается за счет того, что координаты адаптируются к движению горизонта событий, обеспечивая плавное и реалистичное описание гравитационного поля. Такая точность особенно важна при исследовании сложных сценариев, таких как слияние чёрных дыр или аккреция вещества, когда необходимо учитывать все нюансы взаимодействия гравитации и материи. R_{\mu\nu} - \frac{1}{2}g_{\mu\nu}R + \Lambda g_{\mu\nu} = \frac{8\pi G}{c^4}T_{\mu\nu} Возможность детального моделирования динамики чёрных дыр с помощью этих координат открывает новые перспективы для проверки теорий гравитации и изучения экстремальных астрофизических явлений.
Масса Миснера-Шарпа представляет собой ключевой инструмент для количественной оценки энергии, заключенной внутри горизонта событий чёрной дыры. В отличие от традиционных понятий массы, она учитывает как энергию гравитационного поля, так и энергию, содержащуюся в материи, находящейся внутри горизонта. Этот подход особенно важен при моделировании динамики чёрных дыр, поскольку позволяет более точно описывать их эволюцию и взаимодействие с окружающим пространством. M = \frac{r}{2} (1 - \frac{2GM}{rc^2}) — данная формула позволяет вычислить массу Миснера-Шарпа в координатах Painlevé-Gullstrand, где r — радиальная координата, G — гравитационная постоянная, а c — скорость света. Использование этой массы позволяет учёным исследовать физические процессы, происходящие вблизи и внутри чёрных дыр, и лучше понимать природу гравитации.
Усовершенствованные возможности моделирования, предоставляемые координатами Палевена-Гуллстренда, открывают новые перспективы для глубокого понимания гравитационных явлений и изучения экстремальных компактных объектов. Традиционные подходы часто сталкиваются с ограничениями при описании сильных гравитационных полей, однако данный метод позволяет с высокой точностью исследовать динамику чёрных дыр и других объектов с экстремальной плотностью. Это особенно важно для изучения таких явлений, как гравитационные волны, аккреция вещества на компактные объекты и даже возможность существования экзотических структур, выходящих за рамки классического понимания чёрных дыр, таких как звёзды с голыми сингулярностями или червоточины. Повышенная точность моделирования позволяет не только подтверждать предсказания общей теории относительности в экстремальных условиях, но и выявлять потенциальные отклонения, которые могут указывать на необходимость пересмотра фундаментальных физических теорий.
Исследование демонстрирует, что релаксация чёрных дыр после возмущения может проявлять неожиданную ‘бутылочную’ фазу, обусловленную внутренней нелинейностью. Этот процесс, как показывает работа, приводит к задержке излучения гравитационных волн, что противоречит ожидаемому немедленному затуханию. В этом контексте, слова Галилея: «Всё в этом мире подчинено математическим законам», приобретают особое значение. Нелинейность, выявляемая в динамике чёрных дыр, является проявлением этих законов, и понимание её позволяет раскрыть тонкости поведения этих загадочных объектов. Элегантность математического описания, как и в данном исследовании, делает систему более понятной и человечной.
Куда Ведёт Этот Лабиринт?
Исследование, подобно тщательно настроенному инструменту, выявило неожиданную гармонию в кажущемся хаосе релаксации чёрных дыр. Элегантность этой «бутылочной шейки», возникающей из нелинейностей, заставляет задуматься: не является ли это лишь первым аккордом в симфонии, которую мы ещё не слышим? Поиск других проявлений подобного «застревания» — не только в гравитационных волнах, но и в иных областях нелинейной динамики — представляется ключевой задачей. Всё же, необходимо признать, что используемые упрощения — как и всегда — накладывают отпечаток на результат.
Особый интерес представляет вопрос о влиянии спина чёрной дыры на наблюдаемую динамику. Подобно тому, как скрипка звучит иначе в руках виртуоза, вращение может существенно изменить форму и продолжительность этого «застревания». Более того, анализ устойчивости полученных решений к малым возмущениям, и особенно, к флуктуациям квантового вакуума, необходимо провести с особой тщательностью. Ведь даже самая тонкая струна может оборваться, если её слишком сильно натянуть.
В конечном итоге, изучение «призрачной» динамики, скрывающейся за горизонтом событий, представляет собой не просто задачу астрофизики, но и проверку фундаментальных принципов, лежащих в основе нашего понимания пространства и времени. Подобно тому, как художник стремится к совершенству в каждой детали, даже незаметной на первый взгляд, мы должны продолжать искать гармонию в кажущемся хаосе Вселенной.
Оригинал статьи: https://arxiv.org/pdf/2602.12101.pdf
Связаться с автором: https://www.linkedin.com/in/avetisyan/
Смотрите также:
- Галактика как ключ к пониманию Вселенной
- Тёмная энергия: новые сигналы из глубин Вселенной
- За гранью Стандартной модели: новые ограничения на взаимодействия нейтрино
- Карты неба: Новый взгляд на крупномасштабную структуру Вселенной
- Космологический парадокс: что не так с расширением Вселенной?
- Разгадка Напряженности Хаббла: Новая Модель Термического Вакуума
- Радиоэхо столкновений: активные ядра галактик в слиящихся группах
- Космические нити рождения звёзд: обнаружены структуры в плотных облаках
- Танцующие тени: вращение экзотических компактных объектов
- Вселенная в фокусе: Новый взгляд на постоянную Хаббла
2026-02-14 09:38