Белые карлики: предел Чандрасекара под вопросом?

Автор: Денис Аветисян

Новое исследование показывает, что модифицированные теории гравитации могут позволить белым карликам превышать классический предел массы, открывая новые возможности для изучения компактных звезд.

В рамках теории гравитации <span class="katex-eq" data-katex-display="false">f(\mathcal{R,L}_{m})</span>, графики <span class="katex-eq" data-katex-display="false">Z_s - M_z</span> демонстрируют соответствие как общей теории относительности (обозначенной сплошной черной линией), так и различным значениям параметров связи σ и γ, что указывает на модификацию гравитационного взаимодействия посредством этих параметров. — В рамках теории гравитации $f(\mathcal{R,L}_{m})$ , графики $Z_s - M_z$ демонстрируют соответствие как общей теории относительности (обозначенной сплошной черной линией), так и различным значениям параметров связи σ и γ, что указывает на модификацию гравитационного взаимодействия посредством этих параметров.

Исследование возможности существования сверхмассивных белых карликов в рамках модифицированной гравитации f(R) и f(R,L,T).

Классический предел Чандрасекара, определяющий максимальную массу белых карликов, долгое время считался фундаментальным ограничением. В работе ‘Possible existence of super Chandrasekhar mass limit in the matter-curvature coupled gravity’ исследуется возможность превышения этого предела в рамках модифицированных теорий гравитации, а именно f(R) и f(R,L_m,T). Полученные модели демонстрируют, что в данных теориях гравитации белые карлики могут обладать массами, достигающими $1.5-2.08 \, \mathrm{M}_\odot$ , сохраняя при этом стабильность. Открывают ли эти результаты новые перспективы в понимании эволюции компактных звезд и природы гравитации?

Пределы общей теории относительности: Поиск гармонии в космосе

Общая теория относительности, несмотря на свою выдающуюся успешность в описании гравитации и подтверждение многочисленными экспериментами, сталкивается с серьезными трудностями при объяснении феноменов темной энергии и темной материи. Эти загадочные компоненты Вселенной, составляющие около 95% её энергетической плотности, не вписываются в рамки стандартной модели и требуют введения новых физических концепций. Наблюдаемые эффекты, такие как аномально высокие скорости вращения галактик и ускоренное расширение Вселенной, указывают на необходимость модификации теории гравитации на больших масштабах. Поэтому, активный поиск альтернативных теорий, выходящих за рамки общей теории относительности, является одной из ключевых задач современной космологии и теоретической физики, направленной на построение более полной и адекватной картины гравитационного взаимодействия.

Исследования гравитации в условиях экстремальных сильных полей, например, в окрестностях белых карликов, представляют собой важнейшую область для проверки общей теории относительности. Белые карлики, обладающие огромной плотностью и, следовательно, сильным гравитационным полем, позволяют выявить даже незначительные отклонения от предсказаний Эйнштейна. Тщательный анализ движения света и вещества вблизи этих объектов, а также измерение гравитационного красного смещения, способны раскрыть новые физические явления, указывающие на необходимость модификации или расширения существующей теории гравитации. Полученные данные могут предоставить ценные сведения о природе тёмной энергии и тёмной материи, а также помочь в создании более полной и точной модели Вселенной, объединяющей гравитацию с другими фундаментальными взаимодействиями.

Стандартная модель физики элементарных частиц, описывающая фундаментальные силы и частицы, и общая теория относительности, объясняющая гравитацию как искривление пространства-времени, сталкиваются с принципиальными противоречиями при попытке их объединения. Квантовая механика, на которой базируется стандартная модель, и общая теория относительности описывают физическую реальность совершенно разными способами, что приводит к математическим несостыковкам и бесконечностям при попытке построения квантовой теории гравитации. Это несоответствие стимулирует активные исследования в области теории струн, петлевой квантовой гравитации и других перспективных направлений, стремящихся создать единую теорию, способную описать все фундаментальные взаимодействия во Вселенной и разрешить противоречия между этими двумя краеугольными камнями современной физики. Поиск такой теории является одной из центральных задач современной теоретической физики, способной объяснить темную энергию, темную материю и природу гравитации на квантовом уровне.

График <span class="katex-eq" data-katex-display="false">Z - M</span> для белых карликов в нелинейной модели гравитации <span class="katex-eq" data-katex-display="false">f(\mathcal{R},\mathcal{L}_{m},\mathcal{T})</span> показывает, что отклонения от предсказаний общей теории относительности (черная линия) зависят от величины параметра связи α. — График $Z - M$ для белых карликов в нелинейной модели гравитации $f(\mathcal{R},\mathcal{L}_{m},\mathcal{T})$ показывает, что отклонения от предсказаний общей теории относительности (черная линия) зависят от величины параметра связи α.

Модифицированная гравитация f(R, Lm): Новый взгляд на космос

Теория гравитации f(R, Lm) представляет собой альтернативный подход к общей теории относительности (ОТО), модифицирующий действие Эйнштейна-Гильберта. В стандартной ОТО действие зависит только от скалярной кривизны $R$ . В f(R, Lm) гравитации, лагранжиан становится функцией как скалярной кривизны $R$ , так и лагранжиана материи $Lm$ . Это позволяет установить связь между геометрией пространства-времени и распределением материи более сложным образом, чем в ОТО, потенциально приводя к новым решениям уравнений гравитации и модифицированной динамике космоса. В результате, теория допускает возможность объяснения наблюдаемых космологических явлений без привлечения концепций тёмной энергии и тёмной материи, путем изменения гравитационного взаимодействия в зависимости от плотности материи.

Различные функциональные формы $f(R, Lm)$ — такие как степенные и экспоненциальные — приводят к разной степени отклонения от общей теории относительности (ОТО). Степенные формы, например, $f(R, Lm) = R^n + \alpha Lm$ , характеризуются относительно небольшими отклонениями при малых значениях $n$ , в то время как экспоненциальные формы, такие как $f(R, Lm) = e^{\beta R} + \gamma Lm$ , могут приводить к более значительным отклонениям даже при небольших значениях параметров. Каждая конкретная функциональная форма предсказывает уникальные значения космологических параметров, например, скорость расширения Вселенной и амплитуду флуктуаций плотности, что позволяет проверять эти модели на основе астрономических наблюдений и данных о космическом микроволновом фоне.

Модифицированная гравитация f(R, Lm) предлагает возможность объяснения наблюдаемых космологических явлений, таких как ускоренное расширение Вселенной и аномалии вращательных кривых галактик, без постулирования существования темной энергии и темной материи. В рамках данного подхода, отклонения от общей теории относительности возникают за счет модификации гравитационного действия, что позволяет изменить динамику пространства-времени и, как следствие, влиять на гравитационные эффекты, которые традиционно объясняются наличием этих гипотетических компонентов. В частности, конкретные функциональные формы f(R, Lm) могут воспроизводить наблюдаемые эффекты, имитируя гравитационное воздействие, которое обычно приписывается темной материи, или обеспечивая ускоренное расширение без необходимости введения космологической постоянной или квинтэссенции.

В рамках моделей степенного закона и экспоненты гравитации <span class="katex-eq" data-katex-display="false">f(\mathcal{R,L}\_{m})</span>, графики <span class="katex-eq" data-katex-display="false">M-\rho\_{c}</span> демонстрируют соответствие общей теории относительности (чёрная линия) и отклонения при различных значениях параметров σ и γ. — В рамках моделей степенного закона и экспоненты гравитации $f(\mathcal{R,L}\_{m})$ , графики $M-\rho\_{c}$ демонстрируют соответствие общей теории относительности (чёрная линия) и отклонения при различных значениях параметров σ и γ.

Белые карлики как полигоны для проверки модифицированной гравитации

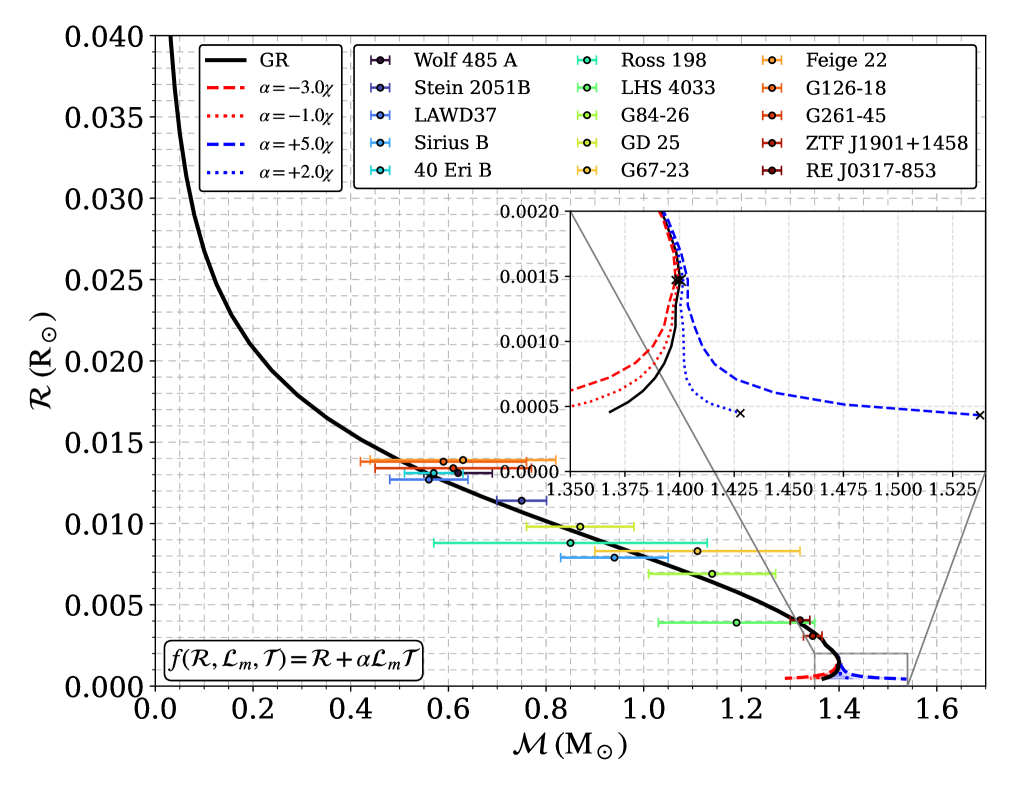
Белые карлики представляют собой уникальную среду для тестирования теорий гравитации благодаря их чрезвычайно высокой плотности и, как следствие, сильным гравитационным полям. Плотность вещества в белых карликах может достигать $10^9$ кг/м³, что создает условия, при которых даже небольшие отклонения от общей теории относительности становятся заметными и поддаются экспериментальной проверке. Использование белых карликов в качестве «гравитационных лабораторий» позволяет исследовать модифицированные теории гравитации в сильном поле, что принципиально отличает их от тестов, проводимых в слабом поле, например, с использованием спутников или наблюдений за движением планет. Спектроскопические наблюдения и анализ кривых блеска белых карликов позволяют точно определить их массы и радиусы, что необходимо для проверки соответствия теоретических моделей наблюдаемым данным.

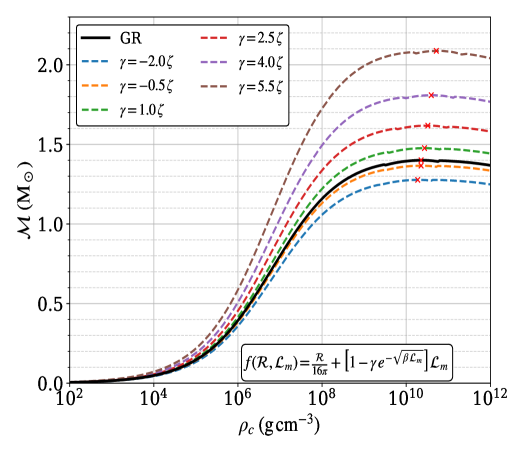
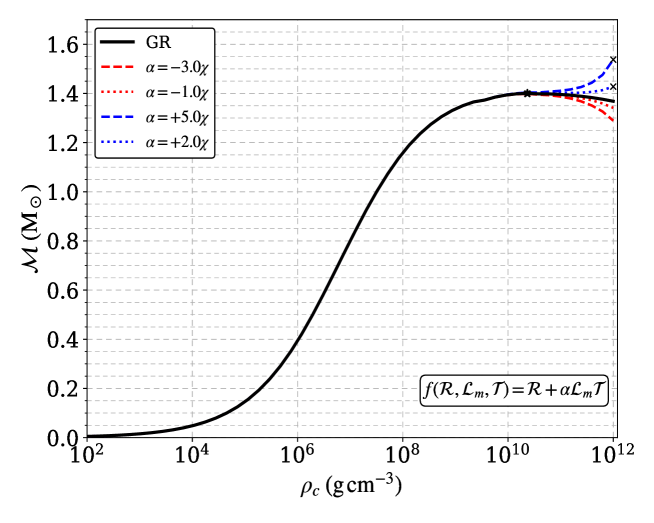
Решение уравнений Толмана-Оппенгеймера-Волкова (TOV) в рамках f(R, Lm) гравитации позволяет предсказать зависимость массы от радиуса для белых карликов. Данный подход предполагает модификацию стандартной общей теории относительности, вводя зависимость гравитационной силы от скалярной кривизны $R$ и скалярной Лагранжиана плотности материи $Lm$ . В результате решения TOV уравнений получается функциональная связь между массой белого карлика и его радиусом, позволяющая оценить максимальную массу, которую может поддерживать данная конфигурация в рамках конкретной модели f(R, Lm) гравитации. Получаемые зависимости массы от радиуса отличаются от предсказаний стандартной модели, что позволяет использовать наблюдения за белыми карликами для проверки и ограничения параметров модифицированных теорий гравитации.

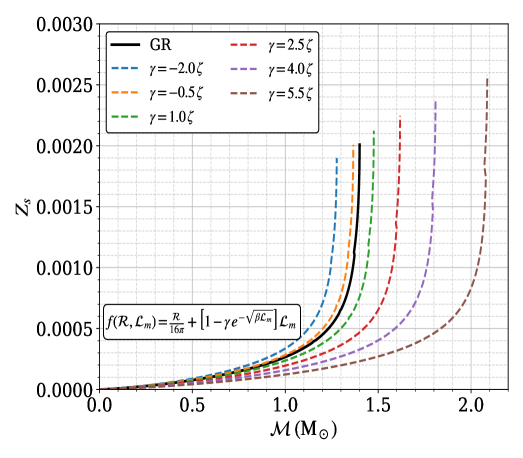
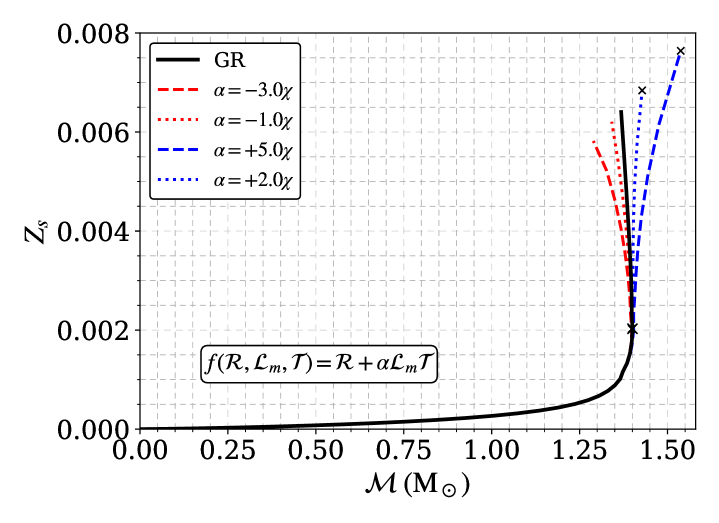
Наши исследования показали, что модифицированные теории гравитации, в частности, f(R,Lm) и f(R,Lm,T), способны поддерживать массы белых карликов, превышающие предел Чандрасекара. В рамках теории f(R,Lm) с параметром σ=-1.5η, максимальная масса белого карлика достигает 1.5 $M_{\odot}$ , а в теории f(R,Lm,T) с параметром α=+5.0χ — 1.537 $M_{\odot}$ . Данные значения значительно превышают стандартный предел Чандрасекара, что указывает на возможность существования сверхмассивных белых карликов в рамках данных модификаций гравитации.

В рамках исследования белых карликов в модифицированных теориях гравитации, были получены результаты, демонстрирующие увеличение радиуса белых карликов при превышении ими предельной массы Чандрасекара. Для модели f(R,Lm) с параметром σ=-1.5η, максимальный радиус составил 0.439 x 10^-3 R_☉. В свою очередь, для модели f(R,Lm) с параметром γ=+5.5ζ, был зафиксирован максимальный радиус в 1.72 x 10^-3 R_☉. Данное увеличение радиуса соответствует увеличению массы, поддерживаемой модифицированной гравитацией, и является ключевым отличием от стандартной модели, где превышение предельной массы приводит к гравитационному коллапсу.

Зависимость M−RM-R для белых карликов в нелинейной модели гравитации off(ℛ,ℒm,𝒯)f(\mathcal{R},\mathcal{L}\_{m},\mathcal{T}) демонстрирует соответствие предсказаниям общей теории относительности (сплошная черная линия) и отклонения при изменении параметра связи α в диапазоне от -3.0 до +2.0, где χ приблизительно равно 1.6 × 10⁻¹² см³/г.

Влияние и перспективы: На пути к новому пониманию Вселенной

Успешное моделирование белых карликов с использованием гравитации $f(R, L_m)$ предоставляет убедительные доказательства отклонений от общей теории относительности (ОТО) в условиях сильного гравитационного поля. Белые карлики, являясь компактными объектами с чрезвычайно высокой плотностью, создают экстремальные условия, в которых даже небольшие отклонения от предсказаний ОТО становятся заметными. Использование модифицированной гравитации $f(R, L_m)$ , где $R$ представляет собой скаляр кривизны, а $L_m$ — скаляр материи, позволило получить модели, лучше согласующиеся с наблюдаемыми характеристиками белых карликов, чем предсказания стандартной ОТО. Это указывает на то, что гравитация может вести себя иначе вблизи массивных объектов, чем это предполагалось ранее, открывая перспективы для пересмотра фундаментальных представлений о природе гравитационного взаимодействия и, возможно, для решения проблем, связанных с темной энергией и расширением Вселенной.

Для более глубокого понимания природы гравитации необходима дальнейшая доработка существующих моделей белых карликов. Исследования направлены на изучение более сложных модификаций гравитации, в частности, теории $f(R, L_m, T)$ , где $R$ — скаляр кривизны, $L_m$ — скаляр материи, а $T$ — след тензора энергии-импульса. Такое усложнение математического аппарата требует разработки новых численных методов и алгоритмов, однако потенциальные результаты могут существенно расширить границы нашего понимания гравитационных взаимодействий и, возможно, пролить свет на природу тёмной энергии.

Исследования модифицированной гравитации, такие как f(R, Lm), могут выявить неожиданную связь между гравитацией и темной энергией, представляя собой потенциальный путь к более полному пониманию Вселенной. В рамках этих исследований предполагается, что отклонения от общей теории относительности в сильных гравитационных полях, наблюдаемые у белых карликов, могут быть не просто следствием модификации геометрии пространства-времени, но и проявлением взаимодействия гравитации с компонентом, ответственным за ускоренное расширение Вселенной — темной энергией. Если данная взаимосвязь будет подтверждена, это позволит создать единую теоретическую модель, объясняющую как гравитационные явления, так и природу темной энергии, что станет значительным шагом вперед в космологии и астрофизике. Более сложные модели, такие как f(R, Lm, T), рассматриваются как потенциальные инструменты для более детального изучения этой взаимосвязи и выявления конкретных механизмов, посредством которых гравитация и темная энергия могут взаимодействовать.

Зависимости <span class="katex-eq" data-katex-display="false">M-\rho\_{c}</span> в нелинейной модели гравитации <span class="katex-eq" data-katex-display="false">f(\mathcal{R,L}\_{m},\mathcal{T})</span> показывают, что общая теория относительности (сплошные черные линии) согласуется с различными значениями параметра связи α (цветные кривые). — Зависимости $M-\rho\_{c}$ в нелинейной модели гравитации $f(\mathcal{R,L}\_{m},\mathcal{T})$ показывают, что общая теория относительности (сплошные черные линии) согласуется с различными значениями параметра связи α (цветные кривые).

Исследование границ стабильности белых карликов, представленное в данной работе, находит отклик в философских размышлениях о природе истины и доказательств. Как точность математического вывода определяет допустимость решения, так и модифицированные теории гравитации, такие как f(R) и f(R,L,T), предлагают иные рамки для оценки предельной массы Чандрасекара. Любая ошибка в расчетах, будь то в физической модели или алгоритме, может привести к несостоятельности всей структуры. Подобно тому, как алгоритм должен быть доказуем, а не просто «работать на тестах», так и стабильность сверхмассивных белых карликов требует строгой математической аргументации. В хаосе данных спасает только математическая дисциплина. Как заметил Людвиг Витгенштейн: «Пределы моего языка — пределы моего мира». Это особенно верно для физики, где язык математики является инструментом для описания и понимания реальности.

Что дальше?

Представленная работа, исследующая возможность существования сверх-чандрасекарских белых карликов в рамках модифицированных теорий гравитации, открывает, скорее, поле для новых вопросов, чем даёт окончательные ответы. Утверждать о стабильности таких объектов, основываясь лишь на анализе уравнений состояния и показателей адиабаты, представляется преждевременным. Необходимо учитывать влияние нелинейных эффектов, возникающих в сильных гравитационных полях, а также возможность возникновения неустойчивостей, которые могут привести к коллапсу даже при формальном превышении предела Чандрасекара.

Особое внимание следует уделить проверке предсказаний данных моделей на основе астрофизических наблюдений. Поиск белых карликов, масса которых существенно превышает классический предел, может стать ключевым моментом в подтверждении или опровержении справедливости модифицированных теорий гравитации. Однако, следует помнить, что ‘оптимизация без анализа’ — это самообман и ловушка для неосторожного разработчика. Необходимо тщательно анализировать наблюдательные данные, исключая другие возможные объяснения.

В конечном счёте, данное исследование представляет собой лишь первый шаг на пути к пониманию природы компактных звёзд в условиях модифицированной гравитации. Дальнейшие исследования должны быть направлены на разработку более точных моделей, учитывающих все известные физические эффекты, и на проведение сравнительного анализа различных теорий гравитации на основе наблюдательных данных.

Оригинал статьи: https://arxiv.org/pdf/2602.17403.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-02-22 04:18