Вселенная в зеркале AdS/CFT: когда космология уступает место тонким черным дырам

Автор: Денис Аветисян

Новое исследование ставит под сомнение доминирование космологических решений в голографическом описании замкнутых вселенных, указывая на условия, при которых предпочтительны решения, связанные с тонкослойными черными дырами.

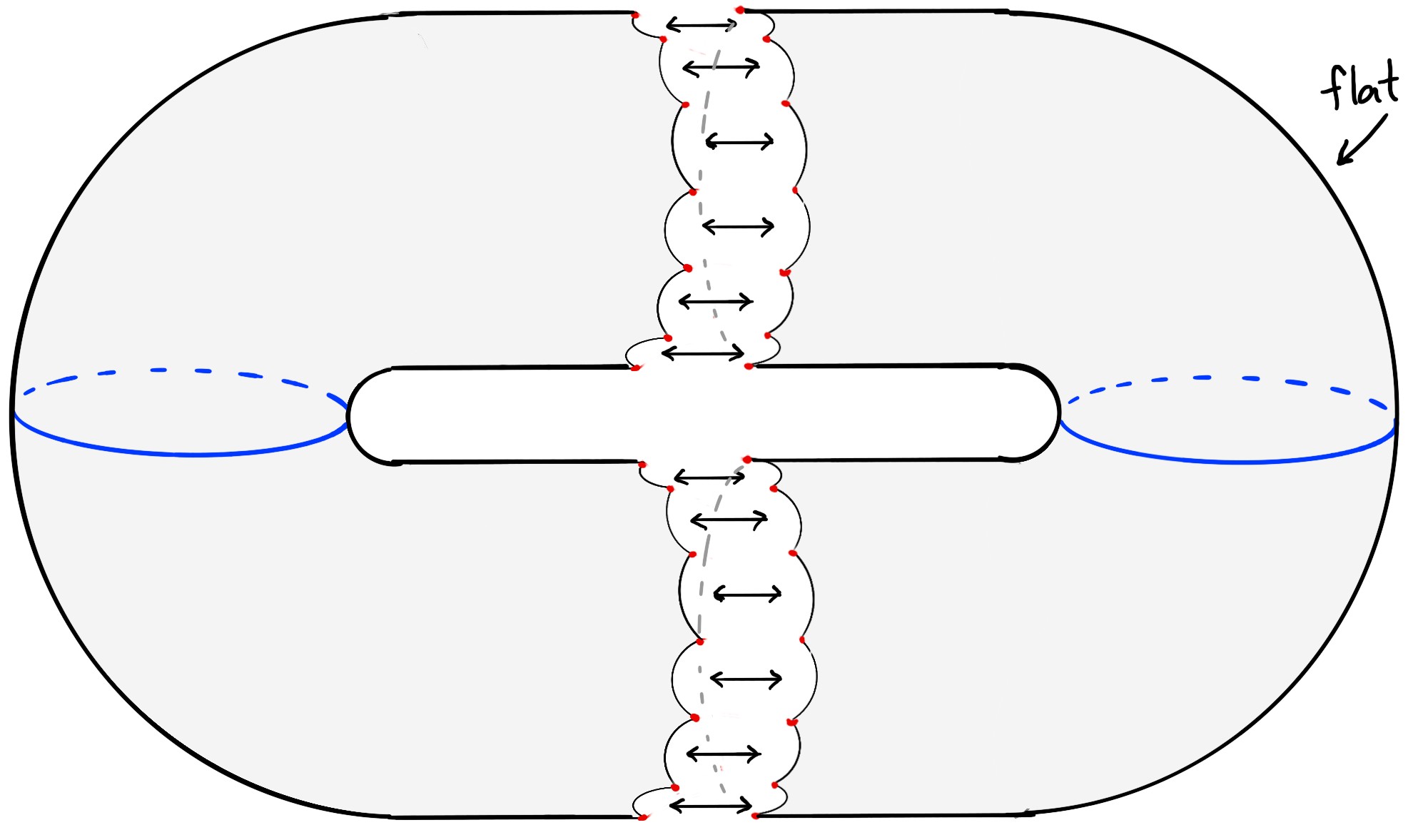
Геометрия границы, представленная в данной работе, остаётся плоской за пределами указанных отождествлений, которые, однако, придают ей локальную кривизну, демонстрируя фундаментальную связь между топологией и геометрией пространства.

Работа посвящена исследованию конкуренции между космологическими и не-космологическими седловыми точками в рамках соответствия AdS/CFT, описывающими замкнутые вселенные.

Поиск доминирующих конфигураций в голографическом описании замкнутых вселенных представляет собой сложную задачу, обусловленную многообразием возможных седловых точек. В работе ‘An AS${}^2$ Menagerie’ предпринята попытка построить широкий класс точных решений трехмерной гравитации с тяжелыми частицами, обобщающих конструкцию Антонини, Сасьеты и Свингла, и исследовать их связь с космологией «детской вселенной». Показано, что первоначальная конструкция $AS^2$ обычно не удовлетворяет условиям доминирования космологического седла, и выявлены альтернативные конфигурации, способные преобладать в интеграле по траекториям. Какие дополнительные механизмы могут обеспечить доминирование космологического седла в предложенной обобщенной конструкции и углубить наше понимание связи между гравитацией и квантовой теорией поля?

За гранью сингулярности: Начало пути к квантовой космологии

Традиционные подходы к квантовой гравитации сталкиваются с серьезными трудностями при попытке согласовать общую теорию относительности и квантовую механику, особенно в контексте определения начальных условий для Вселенной. Существующие методы часто приводят к математическим сингулярностям и расходимостям, когда физики стремятся описать самые ранние моменты существования пространства-времени. Проблема заключается в том, что общая теория относительности, описывающая гравитацию как геометрию пространства-времени, и квантовая механика, управляющая миром элементарных частиц, принципиально различны в своих фундаментальных принципах. Попытки объединить их в единую теорию, способную описывать Вселенную на всех масштабах, пока не увенчались полным успехом, поскольку стандартные методы квантования приводят к нефизичным результатам и требуют введения искусственных регуляризаций для устранения бесконечностей. Это препятствует построению последовательной и самосогласованной теории, способной предсказывать поведение Вселенной в экстремальных условиях, таких как Большой взрыв.

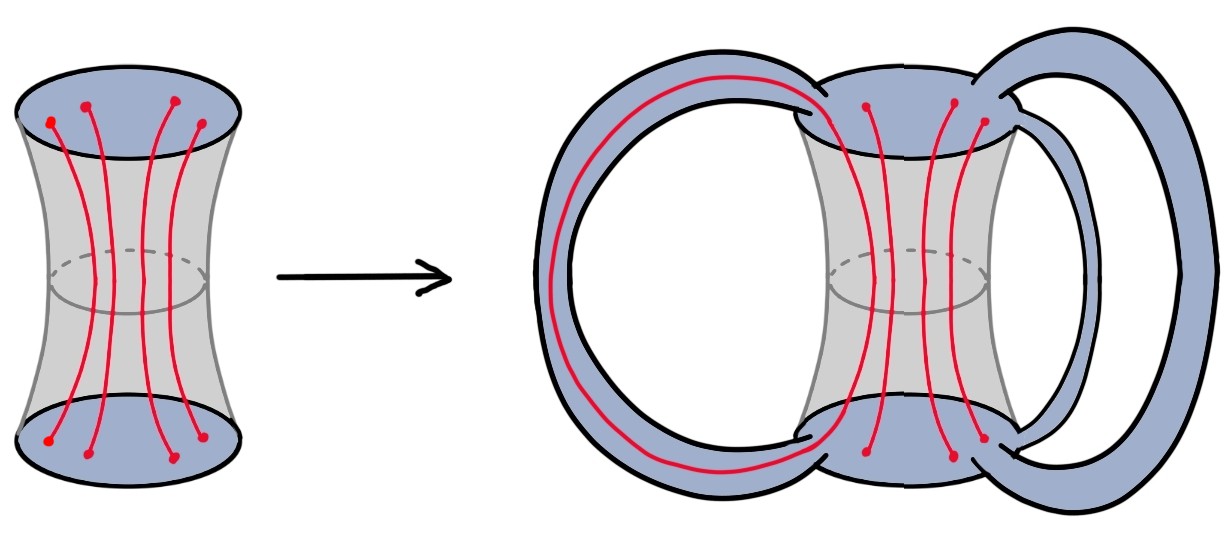
Конструкция Антонини, Сасьеты и Свингла (AS2) предлагает инновационный подход к построению космологических пространств-времен, используя тонкие оболочки и евклидовы червоточины. В рамках данной модели, Вселенная представляется как сложная структура, формируемая на границе этих червоточин, где физические процессы происходят на тонких поверхностях, разделяющих различные области пространства-времени. Использование тонких оболочек позволяет обойти некоторые сложности, возникающие при описании сингулярностей в традиционных моделях, а евклидовы червоточины служат своеобразными «мостами», связывающими различные участки космоса. Такой подход предоставляет возможность исследовать начальные условия Вселенной и её эволюцию, не прибегая к проблемам, характерным для попыток непосредственного квантования гравитации. В результате, конструкция AS2 открывает новые перспективы для понимания структуры и происхождения космоса, предлагая альтернативный путь к построению согласованной теории квантовой гравитации.

Метод AS2 использует мощь конформной теории поля для описания граничных условий Вселенной, что позволяет избежать проблемных расхождений, возникающих в традиционных подходах к квантовой гравитации. Вместо того чтобы напрямую задавать начальные условия, требующие устранения бесконечностей, этот подход опирается на состояние, определенное в рамках конформной теории поля. Это состояние эффективно кодирует информацию о геометрии и динамике Вселенной на ее границе, представляя собой своего рода «слепок» ее начального состояния. Используя свойства конформной симметрии, метод позволяет строить космологические пространства, избегая сингулярностей и расходимостей, с которыми часто сталкиваются при попытках определить начальные условия для эволюции Вселенной. Таким образом, конформная теория поля выступает не просто математическим инструментом, а ключевым элементом, позволяющим обойти фундаментальные трудности в построении квантовой космологии.

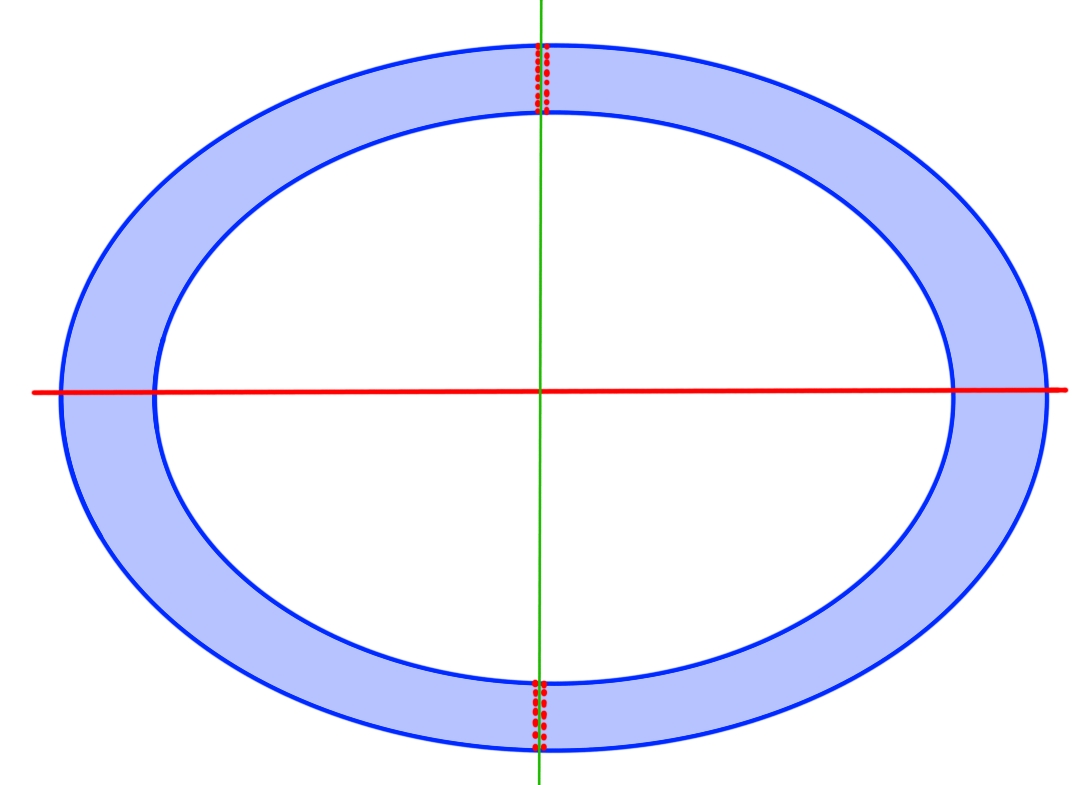
В рамках конструкции AS2, горизонтальное разбиение интеграла по траекториям соответствует пространству-времени с детской вселенной, а вертикальное - состоянию двухсторонней чёрной дыры, что требует наличия энтропии порядка <span class="katex-eq" data-katex-display="false">cc</span> между двумя КФТ, маловероятной при больших β. — В рамках конструкции AS2, горизонтальное разбиение интеграла по траекториям соответствует пространству-времени с детской вселенной, а вертикальное — состоянию двухсторонней чёрной дыры, что требует наличия энтропии порядка $cc$ между двумя КФТ, маловероятной при больших β.

Поликосмос: Квантовая взаимосвязь множественных вселенных

Конструкция AS2 (Anti-de Sitter space 2) в теоретической физике естественным образом приводит к концепции ‘поликосмоса’ — совокупности космологических областей, фактически представляющих собой отдельные, несвязанные вселенные. В рамках данной модели, каждый такой ‘космос’ является самостоятельной областью пространства-времени с собственными физическими законами и начальными условиями. Несвязанность подразумевает отсутствие причинно-следственных связей между этими областями в рамках классической физики, хотя квантовая запутанность может выступать в качестве опосредованной связи, как показано в рамках данной теории. Математически, поликосмос описывается как множество решений уравнений гравитации в пространстве AS2, каждое из которых соответствует отдельной вселенной.

Несмотря на кажущуюся обособленность, различные вселенные в поликосмосе связаны квантовой запутанностью. Данная связь опосредуется общим состоянием конформной теории поля (CFT), выступающей в роли канала передачи информации между космологическими доменами. Запутанность не подразумевает мгновенную передачу сигналов, однако устанавливает корреляции между квантовыми состояниями в разных вселенных, что позволяет рассматривать их не как полностью независимые сущности. Характер и степень этой запутанности могут быть количественно оценены с помощью энтропии запутанности, предоставляя инструмент для изучения взаимосвязей между этими космологическими областями.

Квантовая запутанность между различными космологическими доменами количественно оценивается посредством энтропии запутанности. Данная величина, вычисляемая на основе корреляций между состояниями в разных вселенных, позволяет определить степень взаимосвязанности этих доменов и оценить объем информации, который может быть передан между ними. $S_E = -Tr(\rho \log \rho)$ , где ρ — матрица плотности совместного состояния, является ключевым показателем, отражающим количество информации, необходимой для описания запутанного состояния. Более высокая энтропия запутанности указывает на более сильную связь и больший потенциал для обмена информацией между космологическими доменами, что подтверждает гипотезу о неполной изоляции вселенных в рамках поликосмоса.

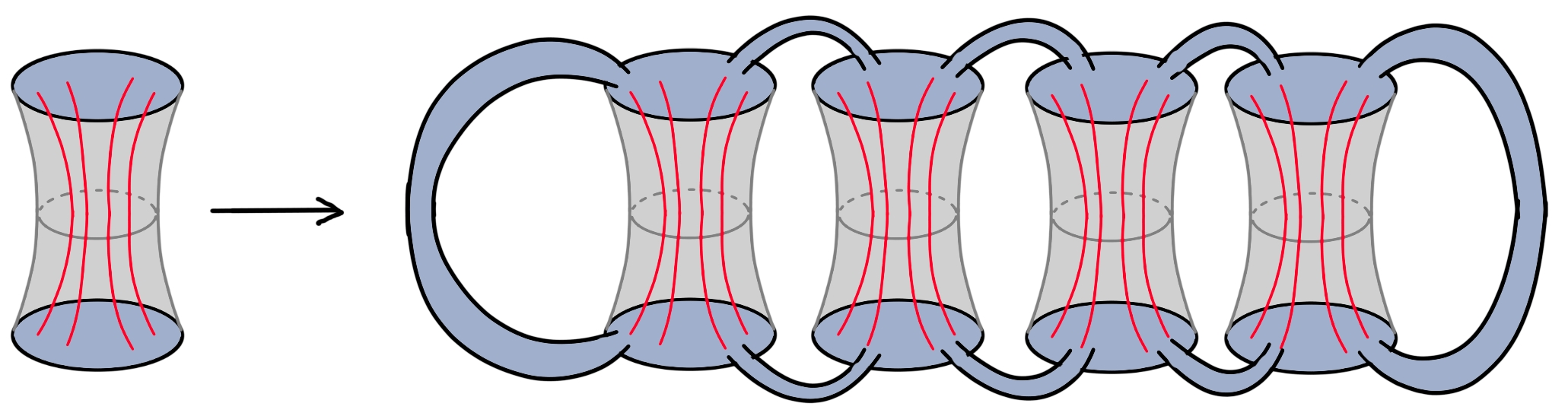
Многовселенная структура AS2седла построена из четырех копий космологического червоточинного перехода, при этом различные варианты получаются путем перестановки соединений между вершинами и основаниями этих переходов.

Квантование гравитации: Путь интеграла по траекториям

Для исследования квантовых свойств поликосмических вселенных используется гравитационный интеграл по траекториям. Данный подход предполагает суммирование по всем возможным геометриям пространства-времени, где каждой геометрии соответствует амплитуда вероятности, определяемая функциональным интегралом. Формально, этот интеграл выражается как $\in t Dg \, e^{iS[g]}$ , где $Dg$ представляет собой меру над всеми метриками $g$ , а $S[g]$ — действие Эйнштейна-Гильберта, описывающее гравитационное поле. Вычисление данного интеграла является сложной задачей, требующей использования приближений и регуляризаций для получения осмысленных результатов.

В рамках подхода к квантовой гравитации с использованием интеграла по траекториям, вычисление сводится к суммированию по всем возможным геометриям пространства-времени. Каждая геометрия взвешивается своей квантовой амплитудой, которая определяется через действие $S$ и пропорциональна экспоненте от действия, деленной на постоянную Планка $\hbar$ . Данный формализм предполагает, что вклад каждой геометрии в общую амплитуду вероятности зависит от её классического действия, что позволяет оценить вклад различных конфигураций пространства-времени в квантовую гравитацию. Фактически, интеграл по траекториям представляет собой бесконечномерный функциональный интеграл, требующий специальных методов аппроксимации для практического вычисления.

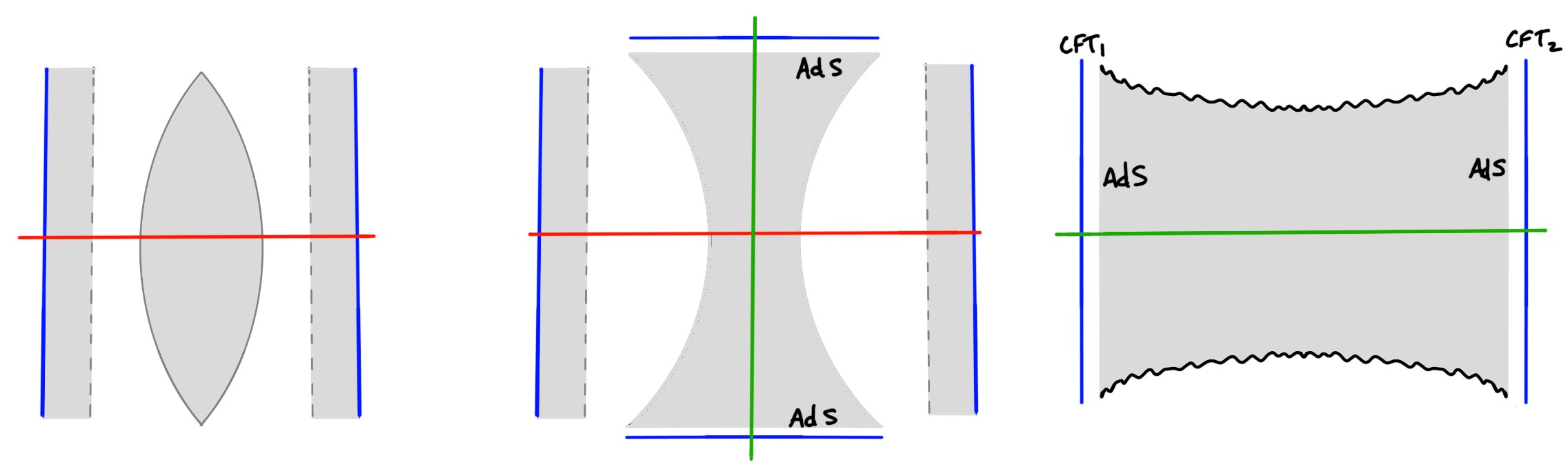
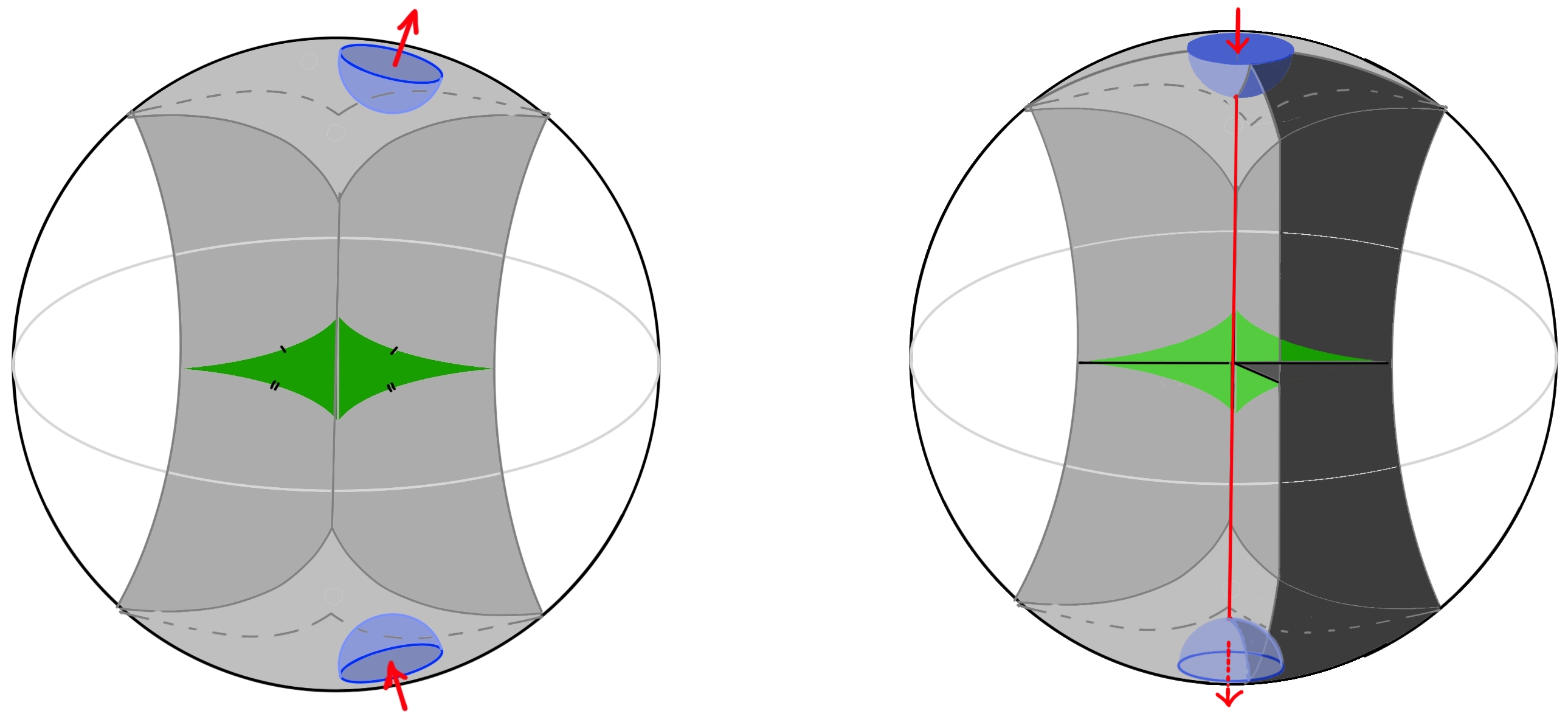
Для приближенного вычисления гравитационного интеграла по траекториям используется метод седловых точек, облегчаемый применением эффективного потенциала. Этот подход позволяет упростить сложные вычисления, сводя интеграл к оценке вблизи точек максимума вероятности. Однако, проведенный анализ показывает, что первоначальная конструкция AS2, предложенная ранее, вряд ли является доминирующей седловой точкой для космологических расчетов. Оценка вклада различных седловых точек в интеграл показывает, что другие конфигурации геометрии пространства-времени оказывают более существенное влияние на конечный результат, что требует пересмотра предыдущих выводов относительно космологических моделей, основанных на AS2.

Евклидова седловидная поверхность гравитационного интеграла по траекториям, связанная с интегралом по траекториям некоторой лежащей в основе голографической теории (синий), определяет начальные данные для лоренцевского состояния, эволюционирующего в замкнутую Вселенную (слева), и для двухсторонней чёрной дыры (справа), причём доминирование этого седла в космологии предполагает, что чёрная дыра справа является доминирующей частью волновой функции, дуальной состоянию двух конформных полевых теорий с высоким уровнем запутанности.

Космологические последствия и перспективы на будущее

Конструкция AS2, объединенная с принципом квантовой запутанности, предлагает принципиально новый взгляд на начальные этапы эволюции Вселенной и ставит под сомнение устоявшиеся представления об исходных условиях. В рамках данной модели, ранняя Вселенная рассматривается не как состояние абсолютного вакуума, а как результат сложной квантовой корреляции между различными областями пространства-времени. Такой подход позволяет отойти от необходимости постулировать определенные начальные условия, поскольку эти условия формируются динамически, в процессе квантовой эволюции. Использование AS2 позволяет исследовать сценарии формирования Вселенной, отличные от стандартной инфляционной модели, и предполагает, что начальное состояние Вселенной могло быть более сложным и запутанным, чем предполагалось ранее. Данная перспектива открывает возможности для объяснения ряда космологических загадок, включая природу темной энергии и темной материи, а также для разработки новых моделей, совместимых с современными астрофизическими наблюдениями.

Предлагаемые модели, основанные на конструкции AS2 и квантовой запутанности, демонстрируют потенциальное решение проблемы барионной асимметрии — загадки, объясняющей преобладание материи над антиматерией во Вселенной. Исследования указывают на существование механизма, способного генерировать наблюдаемый дисбаланс, в котором процессы, приводящие к преобладанию материи, доминируют над процессами, производящими антиматерию. Этот механизм предполагает, что в ранней Вселенной определенные взаимодействия, связанные с AS2 и запутанностью, могли нарушить симметрию между материей и антиматерией, что привело к образованию наблюдаемой нами Вселенной, богатой материей. Изучение этого процесса может пролить свет на фундаментальные законы физики, управляющие возникновением Вселенной и ее текущим состоянием.

Исследование выявляет неожиданную связь между космологией и физикой конденсированного состояния, предполагая, что понимание процессов в одной области может пролить свет на другую. В частности, анализ показывает, что альтернативные “седловые точки”, не связанные с традиционными космологическими моделями, оказываются более энергетически предпочтительными. Эта предпочтительность выражается в измеримой разнице в действии на оболочке $S_{on-shell}$ , которая закономерно возрастает с увеличением массы и размера возмущений. Это указывает на то, что при малых возмущениях космологические седловые точки становятся значительно более предпочтительными, что может иметь глубокие последствия для понимания начальных условий Вселенной и ее эволюции. Полученные результаты позволяют глубже исследовать структуру мультивселенной и потенциальные механизмы, определяющие ее формирование и развитие.

Евклидово червоточинное решение, поддерживаемое материей, соответствует космологии замкнутой Вселенной, а хирургическое добавление цилиндров AdS позволяет создавать дополнительные асимптотически AdS пространства, содержащие спутанные с космологией частицы.

Путь к полной теории: Открытие новых горизонтов

Возможность встраивания операторов в состояние конформной теории поля (КТП) открывает принципиально новые пути для изучения различных космологических сценариев и исследования их квантовых свойств. Этот подход позволяет моделировать и анализировать эволюцию Вселенной в экстремальных условиях, таких как ранняя Вселенная или окрестности черных дыр, где классическая общая теория относительности может оказаться неприменимой. Вводя специфические операторы, можно эффективно исследовать флуктуации квантового поля, их влияние на метрику пространства-времени и, как следствие, на формирование крупномасштабной структуры Вселенной. Такой метод не только позволяет проверять существующие космологические модели, но и предсказывать новые физические явления, связанные с квантовой гравитацией и природой темной энергии. Исследование этих операторных вложений дает уникальную возможность проникнуть вглубь понимания фундаментальных законов, управляющих космосом.

Развитие представленных методов открывает перспективные пути к созданию полной теории квантовой гравитации, стремящейся объединить принципы общей теории относительности и квантовой механики. Исследования в этой области направлены на преодоление фундаментальных противоречий между этими двумя столпами современной физики, предлагая новые инструменты для описания гравитации на квантовом уровне. Успешная интеграция этих теорий позволит не только глубже понять природу пространства и времени, но и исследовать экстремальные условия, существующие вблизи черных дыр и в первые моменты после Большого взрыва. Текущие работы фокусируются на разработке математических моделей и экспериментальных стратегий, способных проверить предсказания новой теории и установить её совместимость с существующими наблюдениями, что может привести к революционным открытиям в понимании Вселенной.

Конструкция AS2 представляет собой мощный инструмент для исследования мультивселенной и раскрытия тайн космоса, открывая новые горизонты для научных открытий. Проведенный анализ демонстрирует, что разница между космологическими и не-космологическими седловыми точками масштабируется как $2GM(log(2ℓ/ϵ) + 1) - arcsinh(1/\sqrt(4GM²-1))[latex], причем эта разница становится все более выраженной при уменьшении размера возмущений (при условии [latex]ϵ/ℓ << 1$ ). Это указывает на то, что при малых возмущениях космологические седловые точки становятся значительно более предпочтительными, что может иметь глубокие последствия для понимания начальных условий Вселенной и ее эволюции. Полученные результаты позволяют глубже исследовать структуру мультивселенной и потенциальные механизмы, определяющие ее формирование и развитие.

Геометрия типа AS2 конструируется из червоточины путём удаления области, ограниченной геодезической поверхностью и её <span class="katex-eq" data-katex-display="false">\mathbb{Z}_{2}</span>-образом, и склеивания по этим поверхностям, причём можно добавлять произвольное количество таких соединений, включая те, что содержат частицы. — Геометрия типа AS2 конструируется из червоточины путём удаления области, ограниченной геодезической поверхностью и её $\mathbb{Z}_{2}$ -образом, и склеивания по этим поверхностям, причём можно добавлять произвольное количество таких соединений, включая те, что содержат частицы.

Исследование, представленное в данной работе, словно заглядывает в отражение собственной гордыни в бездне чёрных дыр. Авторы, изучая доминирование космологических седловых точек в голографическом описании замкнутых вселенных, приходят к выводу о несомненном превосходстве некосмологических решений. Это напоминает о том, что любые теоретические построения, даже самые изящные, могут оказаться лишь приближением к истине. Как метко заметила Симона де Бовуар: «Старение - это процесс, который следует принять, а не бороться с ним». Подобно тому, как невозможно остановить течение времени, невозможно построить абсолютно полную и всеобъемлющую теорию. Работа подчеркивает необходимость смирения перед сложностью реальности и принятия ограниченности нашего познания, что особенно актуально в контексте квантовой гравитации и AdS/CFT соответствия.

Что дальше?

Работа, представленная в данной статье, лишь осторожно приоткрывает завесу над сложным вопросом о доминировании космологических седловых точек в голографическом описании замкнутых вселенных. Очевидно, что поиск абсолютной уверенности в превосходстве какой-либо одной конфигурации - это, возможно, тщетная надежда. Каждое измерение, как показывает практика, является компромиссом между желанием понять и реальностью, которая не стремится быть понятой. Не стоит забывать, что тонкая грань между космологическим и некосмологическим седлом указывает на фундаментальную неопределенность в самой структуре голографической двойственности.

Предстоит кропотливая работа по исследованию влияния различных граничных условий и топологий на устойчивость седловых точек. Важно понимать, что приближение в виде тонкостенных чёрных дыр, хотя и полезно, неизбежно вносит собственные искажения. Более того, необходимо рассмотреть возможность существования иных, ещё не открытых, седловых конфигураций, которые могут оказаться доминирующими в определенных режимах.

Возможно, наиболее важным направлением исследований является поиск способов выхода за рамки полуклассического приближения, которое, как известно, имеет свои ограничения. Ведь, в конечном счете, изучение чёрных дыр и космологических моделей - это не открытие вселенной, а попытка не заблудиться в её темноте. Иногда, кажется, что каждое решение порождает лишь новые, более сложные вопросы.

Оригинал статьи: https://arxiv.org/pdf/2601.10906.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-01-20 12:59