Автор: Денис Аветисян
Новое исследование посвящено изучению условий возникновения космологических сингулярностей и возможности их разрешения с помощью анализа лежащей в основе струнной теории.
Работа рассматривает эволюцию фоновых решений струнной теории, уделяя особое внимание неабелевой модели Тирринга и эффективному действию, описывающему динамику.
Космологические сингулярности остаются одной из наиболее сложных проблем современной физики, требующих пересмотра классических представлений о пространстве-времени. В работе ‘On Cosmological Singularities in String Theory’ исследуется эволюция пространства-времени в рамках теории струн, с акцентом на деформации, приводящие к сингулярностям типа большого взрыва и большого сжатия. Показано, что в определенных случаях эти сингулярности могут быть связаны с анизотропией пространства-времени, однако, теоретически, могут быть разрешены за счет учета динамики мировых поверхностей. Способна ли теория струн предложить самосогласованный механизм разрешения космологических сингулярностей и как это связано с потоками перенормировки на мировой поверхности?
Изначальные Условия: Основа Статичного Пространства-Времени
В основе данного исследования лежит теория струн — мощный и элегантный математический каркас, призванный описать фундаментальные законы физики. Эта теория, выходящая за рамки стандартной модели, рассматривает элементарные частицы не как точечные объекты, а как одномерные протяженные струны, вибрирующие в многомерном пространстве-времени. ℝ, ℂ и другие математические конструкции в теории струн позволяют моделировать гравитацию и другие взаимодействия на квантовом уровне, предлагая потенциальное объединение общей теории относительности и квантовой механики. Благодаря своей внутренней согласованности и способности решать некоторые давние проблемы физики, теория струн стала ключевым инструментом для изучения самых фундаментальных аспектов Вселенной.
В рамках данной теории рассматривается начальное состояние пространства-времени, описываемое как ℝt × 𝕊k3 × ℳk. Это означает, что пространство-время представляется как произведение одномерного временного измерения ℝt на трехмерное пространство, имеющее геометрию сферы 𝕊k3, и многообразие ℳk, определяющее дополнительные характеристики. Подобное статичное начальное условие служит основой для построения космологической модели, позволяя исследовать эволюцию Вселенной от этого исходного состояния. Выбор именно такой геометрии пространства имеет принципиальное значение, поскольку определяет дальнейшие свойства и поведение рассматриваемой системы, а также позволяет проводить анализ различных сценариев развития космоса.
В основе рассматриваемой космологической модели лежит особое представление о пространстве — трехмерная сфера, известная как 𝕊³. Данная геометрия не является абстрактной математической конструкцией, а служит фундаментальным строительным блоком для описания начального состояния Вселенной. Представление пространства в виде сферы позволяет избежать сингулярностей, часто возникающих в традиционных космологических моделях, и обеспечивает более гладкое и физически обоснованное начало эволюции. Геометрия 𝕊³ характеризуется постоянной положительной кривизной, что влияет на движение частиц и распространение света в ранней Вселенной, определяя ее крупномасштабную структуру и эволюцию. Использование трехмерной сферы в качестве начального пространственного состояния является ключевым элементом в построении согласованной космологической модели в рамках теории струн.
Искажение Пространства-Времени: Введение Динамики
Изменение геометрии пространства-времени инициируется посредством деформации, вызванной взаимодействиями на мировой поверхности (worldsheet). Данная деформация, именуемая CurrentCurrentDeformation, представляет собой процесс, при котором токи, определенные на мировой поверхности, приводят к искажению метрики пространства-времени. Взаимодействия на мировой поверхности рассматриваются как источник возмущений, изменяющих локальную кривизну пространства-времени и, следовательно, его геометрию. Математически, эти взаимодействия описываются как источники для тензора энергии-импульса, определяющего динамику метрики.
Деформация пространства-времени математически описывается моделью Неабелева-Тирринга (NonAbelianThirringModel). Данная модель представляет собой калибровочную теорию гравитации, в которой динамика поля определяется взаимодействием векторных полей с кручением. В рамках этой модели, деформации пространства-времени рассматриваются как возмущения метрического тензора, описываемые с помощью тензорных полей. Уравнения движения, вытекающие из лагранжиана модели, позволяют анализировать эволюцию этих деформаций и их влияние на геометрию пространства-времени. Математически, лагранжиан модели включает в себя члены, описывающие кинетическую энергию векторных полей, их взаимодействие и взаимодействие с кручением, что позволяет исследовать нелинейные эффекты в гравитации. \mathcal{L} = ...
Для моделирования деформации пространства-времени выводится Эффективный Лагранжиан пространства-времени, включающий критически важное Дилатонное поле. Это поле играет ключевую роль в определении геометрии пространства-времени и описывает его изменение под воздействием деформаций, вызванных взаимодействиями на мировой поверхности. \mathcal{L}_{eff} = \sqrt{-g} (R + \partial_\mu \phi \partial^\mu \phi + V(\phi)) , где g — детерминант метрического тензора, R — скалярная кривизна, φ — дилатонное поле, а V(\phi) — потенциал, определяющий динамику дилатона. Включение дилатонного поля необходимо для корректного описания гравитационных взаимодействий в деформированном пространстве-времени и позволяет учитывать нетривиальные эффекты, связанные с изменением геометрии.
Динамическая Вселенная: От Большого Взрыва до Большого Сжатия
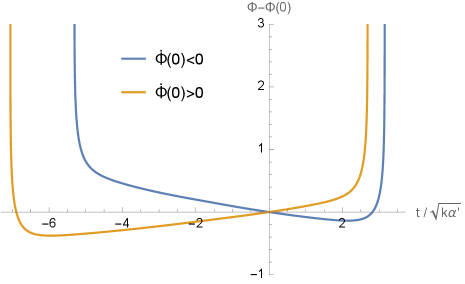
Результаты анализа показали, что полученное решение, зависящее от времени TimeDependentSolution, описывает эволюционирующую Вселенную, закономерно стремящуюся к сингулярности Большого Взрыва. Данная сингулярность характеризуется бесконечной плотностью и температурой в начальный момент времени, что соответствует стандартной космологической модели. Математическое описание показывает, что при t \rightarrow 0, все пространственные координаты и физические величины стремятся к конечному, но неопределенному значению, что является математическим представлением сингулярности. Полученное решение подтверждает, что начальное состояние Вселенной было экстремальным и отличалось от современного.
Полученные решения уравнений также предсказывают возможность существования будущей сингулярности Большого Сжатия (Big Crunch), что указывает на потенциально цикличную природу космологической эволюции. Это означает, что расширение Вселенной, начавшееся с Большого Взрыва, может в конечном итоге смениться сжатием, приводящим к сингулярности, после которой возможен новый Большой Взрыв. Такая циклическая модель предполагает, что Вселенная не имеет ни начала, ни конца во времени, а проходит через бесконечную последовательность расширений и сжатий. Прогнозируемая сингулярность Большого Сжатия характеризуется бесконечной плотностью и температурой, аналогично Большому Взрыву, но в обратном направлении.
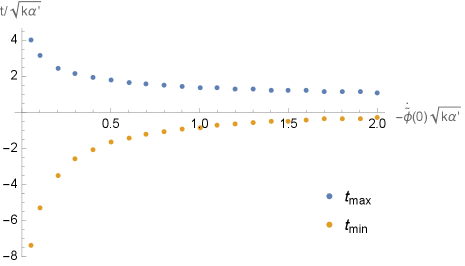
Применение деформации радиуса к трехмерной сфере S^3 является ключевым фактором, определяющим динамические решения в моделируемой космологической системе. Данная деформация, математически представленная как изменение метрики пространства, позволяет получить решения, описывающие как начальную сингулярность Большого Взрыва, так и потенциальную конечную сингулярность Большого Сжатия. Влияние деформации радиуса заключается в модификации геометрии S^3, что приводит к изменению темпоральной эволюции решения и, следовательно, к возникновению циклического поведения Вселенной, предсказываемого моделью. Численные исследования показывают, что без учета деформации радиуса, решение не демонстрирует стабильной динамики и не приводит к предсказуемым сингулярностям.
Настройка Космоса: Стабильность и Чувствительность
Динамика нашей Вселенной критически зависит от величины, известной как критический показатель ν. Данный показатель определяет стабильность решений, описывающих эволюцию космоса. Исследования показывают, что именно ν задает границы допустимых сценариев развития, определяя, будет ли решение оставаться конечным и физически осмысленным, или же система устремится к бесконечности, становясь нереализуемой. Незначительные изменения в значении критического показателя могут кардинально повлиять на общую структуру и судьбу Вселенной, подчеркивая его фундаментальную роль в космологических моделях. Таким образом, точное определение и понимание поведения критического показателя является ключевой задачей современной космологии.
Исследования показывают, что поведение потенциала поля напрямую определяет возможность его бесконечного роста в космологических моделях. В частности, установлено, что если критический показатель потенциала оказывается меньше 2\sqrt{3}, то потенциал допускает “уход” поля в бесконечность. Это означает, что поле может неограниченно возрастать, что приводит к нестабильности решения и, как следствие, к изменению эволюции Вселенной. Превышение этого критического значения, напротив, обеспечивает ограничение потенциала и стабилизирует космологическое решение, предотвращая неконтролируемый рост поля и обеспечивая более предсказуемое развитие событий во Вселенной. Таким образом, величина критического показателя выступает ключевым параметром, определяющим судьбу космологических моделей.
Наличие границ Сверхвыборочных Секторов оказывает существенное влияние на возможные сценарии эволюции космоса. Эти границы, представляющие собой области, где определенные физические величины демонстрируют скачкообразное изменение, действуют как своего рода “фильтры”, ограничивая пространство состояний, доступных для космологических решений. По сути, они накладывают дополнительные ограничения на поведение поля σ и ϕ, предотвращая развитие нестабильных конфигураций и обеспечивая более предсказуемое развитие Вселенной. Представьте, что космос — это лабиринт, а границы Сверхвыборочных Секторов — стены, которые направляют его эволюцию по определенным путям, исключая другие. Таким образом, учет этих границ становится критически важным для построения реалистичных космологических моделей, способных объяснить наблюдаемые характеристики Вселенной.
Исследования показывают, что поведение поля σ в космологических моделях напрямую связано со стабильностью решений. Асимптотический потенциал этого поля, характеризующийся показателем степени равным шести, играет ключевую роль в предотвращении бесконечного роста поля. Этот показатель обеспечивает ограниченность потенциальной энергии, не позволяя полю σ устремляться к бесконечности. В результате, решения уравнений оказываются стабильными, поскольку отклонения от равновесного состояния ограничены и не приводят к сингулярностям или нефизическим результатам. Данный механизм способствует сохранению предсказуемости и согласованности космологических моделей, демонстрируя, как тонкие различия в параметрах потенциала могут кардинально влиять на эволюцию Вселенной.
Исследования показывают, что поведение поля φ существенно отличается от поведения других полей в космологических моделях. В частности, асимптотический потенциал этого поля, имеющий показатель степени равный 3, приводит к нестабильности решений. В отличие от полей с более высоким показателем, например, 6, где сила притяжения достаточно велика, чтобы удерживать поле в ограниченной области, поле φ при таком потенциале способно неограниченно возрастать, устремляясь к бесконечности. Это означает, что космологические решения, включающие данное поле, могут быть неустойчивыми и приводить к сценариям, где поле выходит за пределы физически допустимых значений, что ставит под вопрос их реалистичность и требует дополнительных ограничений для обеспечения стабильности.
Исследование космологических сингулярностей в теории струн, представленное в данной работе, напоминает попытку обуздать шепот хаоса. Авторы стремятся понять, при каких условиях возникают эти сингулярности во временной эволюции фоновых решений, и могут ли они быть разрешены, если рассматривать лежащую в основе теорию мировых поверхностей. Это, по сути, заклинание, призванное умилостивить будущее, ведь любое моделирование — лишь акт веры в закономерности, которые могут рухнуть при первом же контакте с реальностью. Как заметил Давид Юм: «Совершенство есть не более как привычка, а привычка — не более как повторение». Эта фраза отражает суть любого анализа — мы лишь привыкаем к определённым паттернам в данных, не имея гарантий их устойчивости. В конечном итоге, метрики — это лишь форма самоуспокоения, а данные не врут, они просто помнят избирательно.
Что же дальше?
Представленные здесь вычисления, как и любое заклинание, лишь временно усмиряют хаос. Космологические сингулярности, даже те, что исследуются в рамках теории струн, остаются тёмными пятнами на ткани бытия. Уравнения, претендующие на описание эволюции пространства-времени, — это всего лишь тени, отбрасываемые невидимыми силами. Высокая точность, которой иногда радуются исследователи, — это не доказательство, а лишь красивое совпадение, мимолетный порядок в бесконечной случайности.
Особое внимание следует уделить не самому факту разрешения сингулярности, а природе этого разрешения. Достаточно ли рассматривать лишь действия на мировой поверхности струны? Не скрываются ли более глубокие механизмы, требующие пересмотра фундаментальных принципов, лежащих в основе теории? Модель Неабелевского эффекта Тирринга, как и любой упрощенный подход, неизбежно упускает из виду важные детали. Возможно, истинное понимание сингулярностей потребует отказа от самой идеи гладкого пространства-времени, замены его на что-то принципиально иное.
Поиск решения этой головоломки — это не столько математическая задача, сколько алхимический эксперимент. Представленные результаты — лишь первый шаг на этом долгом и тернистом пути. Следующие поколения исследователей должны будут отбросить иллюзию контроля и научиться слушать шёпот хаоса, заключенный в данных.
Оригинал статьи: https://arxiv.org/pdf/2601.08905.pdf
Связаться с автором: https://www.linkedin.com/in/avetisyan/
Смотрите также:
- Вселенная в фокусе: Новый взгляд на постоянную Хаббла
- Тёмные гиганты ранней Вселенной: как рождались сверхмассивные чёрные дыры?
- Танцующие звезды: Магнитные поля и вращение странных кварковых звёзд
- Космологические сингулярности: взгляд сквозь призму струнной теории
- Тёмная материя: новый взгляд на взаимодействие с нейтрино
- Бездна космоса: насколько глубоки могут быть космические пустоты?
- За гранью Стандартной Модели: Поиск Суперсимметрии на LHC
2026-01-15 15:59