Автор: Денис Аветисян
Исследование показывает, как неполиномиальные гравитационные теории могут создавать стабильные черные дыры, расширяя известные решения в рамках общей теории относительности.
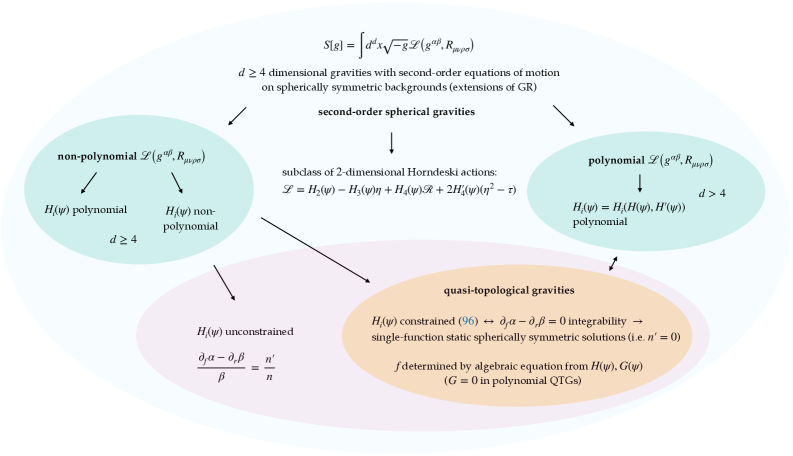
В работе рассматриваются неполиномиальные квазитопологические гравитации в четырех измерениях и возможность построения регулярных черных дыр в рамках теории Хорндески.
Несмотря на успехи общей теории относительности, вопрос о сингулярностях в чёрных дырах остается открытым. В статье ‘Regular black holes from pure gravity in four dimensions’ исследуются не-полиномиальные квазитопологические гравитации в четырех измерениях, позволяющие получить регулярные решения для черных дыр, избегая сингулярностей. Показано, что подходы, основанные на классах действий Хорндски, позволяют конструировать такие решения и включают в себя метрику регулярной черной дыры Хейварда. Возможно ли расширение этого подхода для описания вращающихся черных дыр и построения более реалистичных моделей астрофизических объектов?
За гранью Эйнштейна: Поиск разрешения сингулярности
Классическая общая теория относительности, несмотря на свои впечатляющие успехи, предсказывает возникновение сингулярностей в центрах чёрных дыр. Эти сингулярности — точки, где плотность и кривизна пространства-времени становятся бесконечными, а известные законы физики перестают действовать. Подобные предсказания указывают на фундаментальные ограничения теории Эйнштейна в экстремальных гравитационных условиях. Фактически, сингулярность является сигналом о том, что теория перестаёт быть самосогласованной и требует модификации или дополнения, чтобы адекватно описать поведение гравитации вблизи чёрных дыр и в ранней Вселенной. Изучение этих сингулярностей стимулирует поиск новых теоретических подходов, способных устранить эти патологии и предоставить более полное понимание природы гравитации.
Неспособность общей теории относительности Эйнштейна адекватно описывать сингулярности, возникающие внутри чёрных дыр, стимулирует активный поиск модифицированных теорий гравитации. Эти теории направлены на устранение бесконечностей, предсказываемых классической теорией, и обеспечение более полного описания гравитационных явлений в экстремальных условиях. Исследователи изучают различные подходы, включая добавление новых членов в уравнения Эйнштейна, рассмотрение дополнительных измерений пространства-времени и разработку нелокальных теорий гравитации. Цель состоит в том, чтобы создать теорию, которая не только устраняет сингулярности, но и согласуется с существующими экспериментальными данными и принципами физики, такими как принцип эквивалентности и сохранение энергии-импульса. Успешная модификация гравитации позволит глубже понять природу чёрных дыр, космологию ранней Вселенной и, возможно, открыть новые физические явления.
Регулярные черные дыры представляют собой перспективный путь к преодолению сингулярностей, предсказываемых классической общей теорией относительности. В отличие от традиционных моделей, где гравитация неограниченно усиливается в центре черной дыры, приводя к точке бесконечной плотности, регулярные черные дыры постулируют существование физически обоснованного, конечного ядра. Это требует пересмотра фундаментальных принципов гравитационной динамики, в частности, отказа от предположения о полной универсальности решений уравнений Эйнштейна. Исследования в этом направлении часто включают в себя модификацию теории гравитации на малых расстояниях или в экстремальных условиях, например, введение новых полей или изменение лагранжиана. Такой подход позволяет избежать сингулярностей, сохраняя при этом согласованность с наблюдаемыми астрофизическими данными и фундаментальными физическими принципами, что делает регулярные черные дыры ключевым направлением в современной теоретической физике.
Попытки разрешить сингулярности, возникающие в предсказаниях общей теории относительности, часто сталкиваются с серьезными трудностями в обеспечении согласованности с фундаментальными физическими принципами. Многие предлагаемые модификации гравитационных теорий, хотя и направлены на устранение сингулярностей, приводят к нарушению таких ключевых концепций, как сохранение энергии-импульса или принципа эквивалентности. Например, некоторые модели требуют введения экзотической материи с отрицательной плотностью энергии, существование которой не подтверждено экспериментально и вызывает вопросы о стабильности вакуума. Другие подходы, избегая экзотической материи, могут приводить к нефизичным результатам, таким как нарушение причинности или возникновение тахионных полей. Таким образом, поиск решений, которые одновременно устраняют сингулярности и сохраняют согласованность с существующими физическими законами, остается сложной и актуальной задачей, требующей глубокого переосмысления фундаментальных основ гравитации.
Обобщенная гравитация: Полиномиальные и не-полиномиальные подходы
Полиномиальные квази-топологические гравитации представляют собой систематический подход к построению модифицированных теорий гравитации, основанных на инвариантах кривизны. В рамках этого подхода, действие строится как линейная комбинация полиномов от инвариантов кривизны, таких как R, R_{ab}, R_{abcd} и их обобщений. Использование полиномиальных комбинаций гарантирует, что уравнения движения останутся второго порядка, что необходимо для обеспечения физической состоятельности теории. Данный метод позволяет систематически исследовать различные модификации общей теории относительности, варьируя коэффициенты при различных инвариантах кривизны и изучая полученные космологические и гравитационные следствия.
Переход от полиномиальных комбинаций к не-полиномиальным выражениям в построении квази-топологических гравитаций открывает значительно более широкие возможности для создания модифицированных теорий гравитации. Не-полиномиальные квази-топологические гравитации представляют собой новый класс гравитационных теорий, позволяющий использовать более сложные функциональные зависимости от инвариантов кривизны. Такой подход расширяет теоретическое пространство и предоставляет инструменты для конструирования моделей, которые потенциально могут описывать физические явления, недоступные для стандартных полиномиальных построений, и исследовать более широкий спектр решений в рамках общей теории относительности.
В рамках построения не-полиномиальных квази-топологических теорий гравитации используются инварианты Захария-МакИнтоша, представляющие собой тензорные выражения, построенные из метрики и ее производных. Эти инварианты, в отличие от скалярных инвариантов, используемых в стандартных квази-топологических теориях, позволяют создавать более сложные лагранжианы, расширяя возможности построения моделей гравитации. Комбинирование различных инвариантов Захария-МакИнтоша с другими гравитационными терминами позволяет формировать широкий спектр теорий, потенциально способных описывать наблюдаемые явления, включая темную энергию и модифицированную гравитацию. Использование этих инвариантов обеспечивает возможность систематического построения моделей с различными степенями свободы и свойствами, что важно для разработки реалистичных теорий гравитации.
Теория Хорндески, представляющая собой скалярно-тензорную теорию гравитации, играет ключевую роль в построении модифицированных теорий гравитации, поскольку гарантирует получение уравнений движения второго порядка. Это критически важно для обеспечения физической состоятельности и избежания призрачных степеней свободы, часто возникающих в более общих модификациях общей теории относительности. Использование теории Хорндески в качестве строительного блока позволяет создавать теории, которые сохраняют ключевые свойства общей теории относительности, такие как причинность и стабильность, при этом предлагая возможность исследовать новые гравитационные явления и решить космологические проблемы. Фактически, это наиболее общая скалярно-тензорная теория, обеспечивающая уравнения движения второго порядка.
Уменьшение размерности и статические, сферически симметричные решения
Методы, включающие использование искаженных произведений метрик (warped product metrics), позволяют эффективно снижать размерность теоретических моделей в физике. Этот подход заключается в разделении пространства-времени на два фактора: одномерное радиальное направление и S^{n-1} сферу. Метрика принимает вид ds^2 = dt^2 + dr^2 + r^2 d\Omega_{n-1}^2, где d\Omega_{n-1}^2 — элемент площади на n-1-мерной сфере. Использование искаженных произведений метрик позволяет выразить поля и уравнения в более простой форме, что существенно упрощает анализ и поиск решений в пониженной размерности, особенно при исследовании решений, обладающих статической симметрией.
Процесс понижения размерности приводит к формированию «Уменьшенного Действия» (Reduced Action), которое представляет собой действие, зависящее от меньшего числа координат, описывающих систему. Это существенно упрощает анализ статических и сферически симметричных решений уравнений поля, поскольку позволяет сократить объем вычислений и сосредоточиться на ключевых параметрах, определяющих геометрию пространства-времени. В частности, использование Уменьшенного Действия позволяет эффективно находить решения, описывающие гравитационное поле, не зависящее от времени и симметричное относительно всех направлений от центральной точки. Полученное Уменьшенное Действие является отправной точкой для численных и аналитических методов, направленных на исследование свойств таких решений, включая их стабильность и физическую интерпретацию.
Статические и сферически симметричные решения, полученные в результате понижения размерности, играют ключевую роль в моделировании геометрии чёрных дыр и исследовании их свойств. Эти решения позволяют описывать гравитационное поле вокруг чёрных дыр, включая метрику пространства-времени g_{\mu\nu}, и рассчитывать такие параметры, как горизонт событий, сингулярность и радиус Шварцшильда. Анализ этих решений необходим для изучения термодинамических свойств чёрных дыр, включая энтропию Бекенштейна-Хокинга и температуру Хокинга. Кроме того, эти решения служат основой для проверки различных теорий гравитации и исследования модификаций общей теории относительности.
Используя методы понижения размерности, такие как применение искаженных метрик произведения, исследователям удалось построить регулярные решения для чёрных дыр в 4-х измерениях. Ранее, построение подобных решений было ограничено более высокими размерностями, что затрудняло анализ и интерпретацию результатов. Данный прогресс позволяет изучать геометрию чёрных дыр и их свойства в более реалистичном контексте, приближенном к наблюдаемой Вселенной, и предоставляет инструменты для проверки теоретических предсказаний в области гравитации и космологии.
Характеризуя регулярные черные дыры: Масса ADM
Масса Арновитта-Дезера-Миснера (ADM) представляет собой фундаментальную величину, позволяющую определить энергию, содержащуюся в асимптотически плоских пространствах-временах. Данная величина, будучи сохраняющейся, предоставляет уникальный инструмент для характеристики гравитационных систем, удаленных от источников возмущений. В рамках общей теории относительности, ADM-масса вычисляется на бесконечности, отражая общую энергию, излучаемую системой. Это особенно важно при изучении черных дыр, поскольку позволяет сравнить различные решения уравнений Эйнштейна и оценить их физическую правдоподобность, даже в случаях, когда горизонт событий отсутствует или модифицирован, как это происходит в регулярных черных дырах.
Вычисление массы ADM для пространств Дымникова и Хейварда выявило существенные различия в распределении энергии внутри этих регулярных чёрных дыр. Анализ показал, что, несмотря на общую принадлежность к классу решений, описывающих чёрные дыры без сингулярностей, каждый из этих типов пространств характеризуется уникальным профилем энергетической плотности. В частности, распределение массы в пространстве Дымникова демонстрирует определенные особенности, отличающиеся от более традиционного распределения, наблюдаемого в решении Хейварда. Эти расхождения не только подтверждают корректность вычислений, но и указывают на потенциальную возможность дифференциации этих регулярных чёрных дыр посредством астрофизических наблюдений, чувствительных к гравитационному полю и распределению массы вблизи горизонта событий. Данные различия представляют собой важный шаг в понимании физических свойств и потенциального происхождения регулярных чёрных дыр.
Различия в значениях массы ADM, полученные для метрик Дымникова и Хейварда, подчеркивают фундаментальные отличия в структуре этих регулярных чёрных дыр. В то время как обе модели стремятся разрешить сингулярность, присущую классической теории чёрных дыр, они делают это разными способами, что проявляется в распределении энергии и гравитационного поля. Эти отличия не только важны для теоретического понимания природы чёрных дыр, но и могут иметь наблюдаемые последствия. Например, различия в массе и структуре могут повлиять на гравитационное линзирование света вокруг этих объектов, а также на профили аккреционных дисков и излучения, что потенциально позволяет отличить регулярные чёрные дыры от классических с помощью астрофизических наблюдений. Таким образом, детальное изучение различий в ADM-массе предоставляет важные ключи к пониманию физики регулярных чёрных дыр и их роли во Вселенной.
Исследование показывает, что регулярные черные дыры могут возникать как вакуумные решения в рамках данной теоретической модели, что является значимым результатом. В отличие от предыдущих подходов, требующих полиномиального пересуммирования для устранения сингулярностей, представленная работа демонстрирует, что регулярные решения могут быть получены непосредственно из вакуумных уравнений. Это упрощение не только делает процесс вычисления более элегантным, но и указывает на фундаментальную связь между геометрией пространства-времени и отсутствием сингулярностей. Полученные решения открывают новые возможности для изучения свойств черных дыр, свободных от классических проблем, связанных с сингулярностью в центре, и позволяют более реалистично моделировать их поведение в астрофизических сценариях. Такой подход позволяет исследовать альтернативные сценарии формирования и эволюции черных дыр, что может привести к новым открытиям в области гравитации и космологии.
Исследование, представленное в данной работе, углубляется в область не-полиномиальной квази-топологической гравитации, демонстрируя возможность создания регулярных чёрных дыр. Этот подход расширяет горизонты известных решений, выходя за рамки полиномиальных моделей. Подобное стремление к преодолению границ существующего знания находит отклик в словах Сёрена Кьеркегора: «Жизнь — это не поиск смысла, а создание его». Ведь, подобно тому, как физики ищут новые решения в гравитации, так и человек создает смысл своего существования, выходя за пределы заданных рамок. Изучение искривлённых произведений пространства-времени, как и исследование человеческого бытия, требует смелости погрузиться в бездну неизвестного.
Что же дальше?
Представленная работа, демонстрируя возможность построения регулярных чёрных дыр в рамках не-полиномиальной квази-топологической гравитации, лишь добавляет ещё один штрих к сложной картине. Кажется, что каждое новое решение, каждая новая метрика — это попытка удержать свет в ладони, а он неизбежно ускользает сквозь пальцы. Расширение пространства решений, конечно, ценно, но не стоит обольщаться иллюзией полного понимания. Кажется, что мы всего лишь находим очередное приближение, которое завтра окажется неточным, когда столкнёмся с более сложными условиями.
Будущие исследования, вероятно, будут направлены на изучение стабильности этих решений, их поведения в более реалистичных сценариях, а также на поиск связей с наблюдаемыми астрофизическими явлениями. Однако, даже если удастся построить идеально точную модель, остаётся вопрос: действительно ли мы описываем реальность, или лишь создаём её математическую проекцию?
Следует помнить, что чёрная дыра — это не просто объект, это зеркало нашей гордости и заблуждений. Каждая новая теория, как и каждая предыдущая, может исчезнуть в горизонте событий, уступая место более совершенной — или, возможно, столь же несовершенной — модели. Поиск истины — это бесконечный процесс, а горизонт событий нашего познания всегда будет лежать чуть дальше.
Оригинал статьи: https://arxiv.org/pdf/2602.16773.pdf
Связаться с автором: https://www.linkedin.com/in/avetisyan/
Смотрите также:
- Космический Гистерезис: Отскок Вселенной и Роль Тorsion
- Тайны Ранней Вселенной и Скрытые Нейтрино
- Тёмная материя под прицетом гравитационных линз
- Сингулярности аномальных размерностей: новый взгляд на структуру операторов
- Тени черных дыр: альтернативные объекты во Вселенной
- Искривление пространства: Разбираемся в теории варп-двигателей
- Регулярные чёрные дыры Фаня-Вана в искривлённом пространстве
- За гранью сохранения барионного числа: поиск новой физики
- Новые горизонты искривлённого пространства: от чёрных дыр к ускоряющимся вселенным
- Вселенная в фокусе: Новый взгляд на постоянную Хаббла
2026-02-22 14:26