Автор: Денис Аветисян
Новое исследование показывает, что кажущиеся аномалии в структуре Вселенной, вероятно, являются статистической случайностью, а не свидетельством её анизотропии.
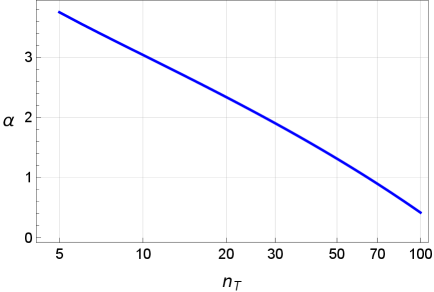
Анализ космического микроволнового фона демонстрирует, что ранее обнаруженные отклонения от модели ΛCDM могут быть объяснены эффектом многократного тестирования.
Недавние утверждения о наличии статистической анизотропии Вселенной, основанные на анализе аномалий космического микроволнового фона, требуют критической оценки. В работе, озаглавленной ‘Statistical isotropy of the universe and the look-elsewhere effect’, авторы утверждают о высокой статистической значимости отклонений от изотропности. Мы показываем, что заявленная значимость существенно переоценена вследствие эффекта множественных сравнений, и что подобный результат вполне ожидаем при большом количестве проведенных тестов против ΛCDM модели. Не ослабляет ли это уверенность в стандартной космологической модели и требует ли более строгого контроля за статистической валидацией обнаруженных аномалий?
Космологические допущения под вопросом
Стандартная ΛCDM-модель, являющаяся основой современных космологических представлений, базируется на фундаментальном предположении о статистической изотропии Вселенной. Это означает, что, в среднем, Вселенная выглядит одинаково во всех направлениях, вне зависимости от точки наблюдения. Иными словами, физические свойства и распределение материи и энергии должны быть однородными при рассмотрении в достаточно больших масштабах. Это допущение существенно упрощает космологические расчеты и позволяет строить предсказания о структуре и эволюции Вселенной. Однако, постоянное совершенствование методов наблюдения и анализа данных заставляет ученых пересматривать даже самые устоявшиеся принципы, и в последнее время появились свидетельства, намекающие на возможные отклонения от идеальной изотропии, что может потребовать пересмотра основных космологических моделей.
Недавние исследования космического микроволнового фона (CMB) указывают на возможные отклонения от изотропности Вселенной, что заставляет ученых пересматривать фундаментальные космологические принципы. Традиционная модель ΛCDM предполагает, что Вселенная выглядит одинаково во всех направлениях, однако анализ CMB демонстрирует намеки на анизотропию — различия в свойствах в разных частях неба. Эти аномалии, хотя и слабые, потенциально свидетельствуют о том, что Вселенная может быть не столь однородной и изотропной, как считалось ранее, что требует более глубокого изучения и, возможно, разработки новых космологических моделей, способных объяснить наблюдаемые отклонения от стандартных представлений. Выявление этих анизотропий требует высокоточных измерений крупномасштабных флуктуаций CMB и тщательного статистического анализа, что представляет собой серьезную научную задачу.
Для проверки статистической изотропии Вселенной необходимы высокоточные измерения крупномасштабных особенностей космического микроволнового фона (CMB) и тщательный статистический анализ полученных данных. Изучение CMB представляет собой сложную задачу, поскольку слабые сигналы могут быть замаскированы различными источниками шума и систематических ошибок. Поэтому, для выявления потенциальных отклонений от изотропии, требуются чувствительные инструменты и передовые методы анализа, способные отделить истинные космические сигналы от артефактов. Тщательное рассмотрение статистической значимости результатов и учет возможных погрешностей является критически важным для получения надежных выводов о крупномасштабной структуре и эволюции Вселенной. Именно поэтому, исследования в этой области требуют сочетания астрономических наблюдений, математического моделирования и статистического анализа.
Анализ, проведенный командой JCSA, предложил инновационный подход к исследованию анизотропии реликтового излучения, объединив несколько независимых тестов, направленных на выявление отклонений от статистической изотропности Вселенной. Вместо использования традиционного анализа отдельных характеристик, исследователи применили комплексную методологию, что позволило им выявить статистически значимые отклонения от ожидаемой изотропности. Первоначальные результаты анализа указывали на наличие асимметрии в крупномасштабной структуре реликтового излучения, что потенциально может потребовать пересмотра стандартной космологической модели ΛCDM и ее фундаментальных предположений о однородности и изотропности Вселенной. Данный подход к анализу реликтового излучения открывает новые возможности для проверки космологических моделей и поиска признаков новой физики за пределами стандартной модели.
Проверка изотропности: Методика и результаты
В анализе JCSA для проверки анизотропии космического микроволнового фона (CMB) использовался комплекс из четырех ключевых тестов. Первый из них измерял дисперсию крупномасштабных температурных анизотропий, определяя степень неоднородности CMB. Второй тест оценивал выравнивание квадрупольного (l=2) и октапольного (l=3) мультиполей, что позволяло выявить предпочтительные направления в CMB. Третий тест исследовал паритетную асимметрию посредством анализа соотношения мощности четных и нечетных мультиполей. Наконец, проводилась оценка согласованности результатов всех четырех тестов для получения комплексной оценки степени анизотропии CMB.
Анализ анизотропии космического микроволнового фона (CMB) требует количественной оценки корреляций в температурных флуктуациях. Для декомпозиции и анализа данных используются матрицы корреляции сферических гармоник, поскольку CMB представляет собой карту температуры на небесной сфере. Сферические гармоники позволяют разложить температурные флуктуации на компоненты различного углового масштаба. Коэффициенты Клебша-Гордана необходимы для правильного преобразования между различными схемами квантования и для вычисления амплитуд этих компонент, учитывая спиновые свойства излучения. Использование этих математических инструментов позволяет выявить статистически значимые корреляции и отклонения от изотропии, что является ключевым для понимания ранней Вселенной и ее структуры.
В ходе анализа JCSA был рассчитан объединенный ‘Коэффициент корреляции’ для оценки общей согласованности четырех тестов на анизотропию космического микроволнового фона (CMB). Этот коэффициент служит единой метрикой степени анизотропии. Оценка эффективного числа независимых тестов, использованных в анализе JCSA, составила 3.26, что было получено на основе коэффициента корреляции, равного 51. Расчет эффективного числа независимых тестов был выполнен с использованием геометрического среднего, что позволило учесть взаимосвязи между результатами отдельных тестов и избежать двойного учета информации.
Эффективность комбинированного подхода к анализу анизотропии космического микроволнового фона (CMB) напрямую зависит от корректного определения числа статистически независимых тестов. В анализе JCSA, для вычисления этого числа использовалось геометрическое среднее. Геометрическое среднее, в отличие от арифметического, позволяет более точно оценить количество независимых измерений, учитывая корреляции между отдельными тестами. В данном случае, геометрическое среднее показало, что эффективное число независимых тестов составляет 3.26, что отражает степень взаимосвязанности между четырьмя проведёнными тестами: анализом дисперсии крупномасштабных анизотропий, оценкой выравнивания квадруполя и октаполя, и проверкой паритетной асимметрии через анализ степеней нечетных и четных мультиполей. Использование арифметического среднего привело бы к переоценке числа независимых тестов, искажая статистическую значимость результатов.
Статистическая строгость и проблема множественных сравнений
При проведении множественных статистических тестов возрастает вероятность обнаружения статистически значимого результата исключительно за счет случайности, что известно как эффект «Look-Elsewhere» (эффект множественных сравнений). Это происходит потому, что при каждом отдельном тесте существует фиксированная вероятность ошибки первого рода (ложноположительного результата), обычно обозначаемая как α. Однако, при увеличении числа независимых тестов, вероятность обнаружения хотя бы одного ложноположительного результата также возрастает. Таким образом, для корректной интерпретации результатов необходимо учитывать поправку на множественные сравнения, чтобы контролировать общую вероятность ошибки первого рода и избежать ошибочных выводов о статистической значимости.
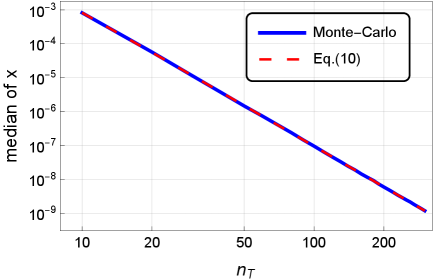
Для решения проблемы учета множественных сравнений, команда JCSA использовала метод Монте-Карло для оценки распределения вероятностей объединенного коэффициента корреляции при условии гипотезы об изотропии. Данный подход заключался в генерации большого числа случайных реализаций данных, соответствующих изотропной модели, и вычислении коэффициента корреляции для каждой реализации. Полученное распределение позволяло оценить вероятность получения наблюдаемого значения коэффициента корреляции, если нулевая гипотеза об изотропии верна. По сути, симуляции создали эталонное распределение, с которым сравнивалось реальное наблюдаемое значение, позволяя оценить статистическую значимость полученных результатов и учесть вероятность ложноположительного результата, возникающего при проведении большого количества статистических тестов.
Команда JCSA использовала методы Монте-Карло для оценки статистической значимости наблюдаемого коэффициента корреляции, учитывая проблему ложноположительных результатов, возникающую при проведении множественных статистических тестов. Суть подхода заключалась в моделировании распределения коэффициента корреляции при условии истинной изотропии (нулевой гипотезы), что позволило определить вероятность получения наблюдаемого или более экстремального значения коэффициента случайным образом. В результате, оценка значимости проводилась с учетом корректировки на количество проведенных тестов, что позволило более точно оценить вероятность реальной анизотропии, а не просто случайного совпадения.
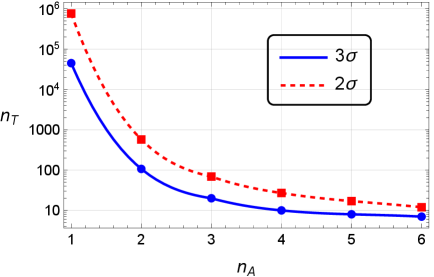
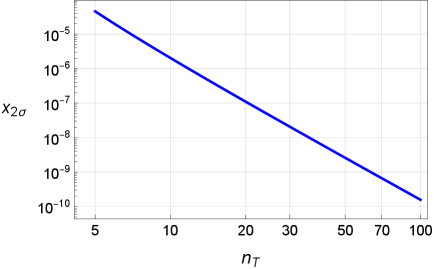
Результаты моделирования Монте-Карло показали, что статистическая значимость заявленной анизотропии снижается при увеличении числа независимых статистических тестов. При рассмотрении 10 независимых тестов, значимость снижается до уровня 3σ, что соответствует вероятности случайного отклонения в 0.3%. Дальнейшее увеличение числа тестов до 27 приводит к снижению значимости до 2σ, что соответствует вероятности случайного отклонения в 4.6%. Эти данные демонстрируют важность учета эффекта множественных сравнений при интерпретации результатов статистического анализа и подчеркивают, что первоначально заявленная статистическая значимость может быть переоценена, если не учитывать общее количество проведенных тестов.
Представленная работа, тщательно анализируя данные космического микроволнового фона, демонстрирует, как легко можно увидеть закономерности там, где их нет. Исследователи показывают, что обнаруженные ранее признаки статистической анизотропии, скорее всего, являются следствием эффекта поиска закономерностей — неизбежного артефакта при проведении множества статистических тестов. Это напоминает о хрупкости любых заключений, основанных на анализе данных. Как заметил Эрвин Шрёдингер: «Невозможно показать, что что-то абсолютно точно». Эта фраза отражает суть исследования: даже самые убедительные свидетельства могут оказаться иллюзией, если не учитывать все факторы, влияющие на процесс наблюдения. По сути, статья указывает на то, что любое измерение — это компромисс между желанием понять и реальностью, которая не хочет быть понята.
Что Дальше?
Представленная работа, демонстрируя влияние эффекта «искания» на интерпретацию статистической изотропии космического микроволнового фона, лишь подчеркивает хрупкость наших заключений о Вселенной. Текущие теории, описывающие космологические модели, такие как ΛCDM, предполагают определенный уровень однородности. Однако, даже математически строгие доказательства могут оказаться иллюзией, если не учитывать множественность проведенных проверок. Возникает закономерный вопрос: не является ли наше стремление к подтверждению ΛCDM моделью самообманом, отражением желания видеть порядок там, где его может и не быть?
Дальнейшие исследования должны быть сосредоточены не только на улучшении точности измерений, но и на разработке более строгих методов статистического анализа. Необходимо учитывать априорные вероятности различных космологических моделей и избегать чрезмерной интерпретации случайных флуктуаций. Текущие подходы к проверке гипотез, основанные на p-значениях, могут быть недостаточны для выявления истинной анизотропии, учитывая сложность и неполноту наших знаний.
В конечном счете, задача космологии — не просто построение математически элегантных теорий, а проверка их соответствия реальности. Необходимо помнить, что горизонт событий наших знаний может оказаться гораздо ближе, чем кажется. Любая модель, даже самая успешная, остается лишь приближением к истине, и её крах — лишь вопрос времени.
Оригинал статьи: https://arxiv.org/pdf/2602.10178.pdf
Связаться с автором: https://www.linkedin.com/in/avetisyan/
Смотрите также:
- Галактика как ключ к пониманию Вселенной
- Разгадка Напряженности Хаббла: Новая Модель Термического Вакуума
- Тёмная энергия: новые сигналы из глубин Вселенной
- За гранью Стандартной модели: новые ограничения на взаимодействия нейтрино
- Космологический парадокс: что не так с расширением Вселенной?
- За гранью Стандартной модели: поиск новых частиц на мюонном коллайдере
- Тёмная материя: скрытая сторона обычного вещества
- Поиск суперсимметрии: новый взгляд на топы и надежды Большого адронного коллайдера
- Космический горизонт: что скрывает аномалия в данных CatWISE?
- Вселенная не так однородна, как кажется: новые данные о космической анизотропии
2026-02-12 18:52