Геометрии пространства и границы космологических моделей

Автор: Денис Аветисян

Новое исследование рассматривает альтернативные геометрии пространства, предложенные Уильямом Тёрстоном, и их соответствие данным о сверхновых типа Ia и космическом микроволновом фоне.

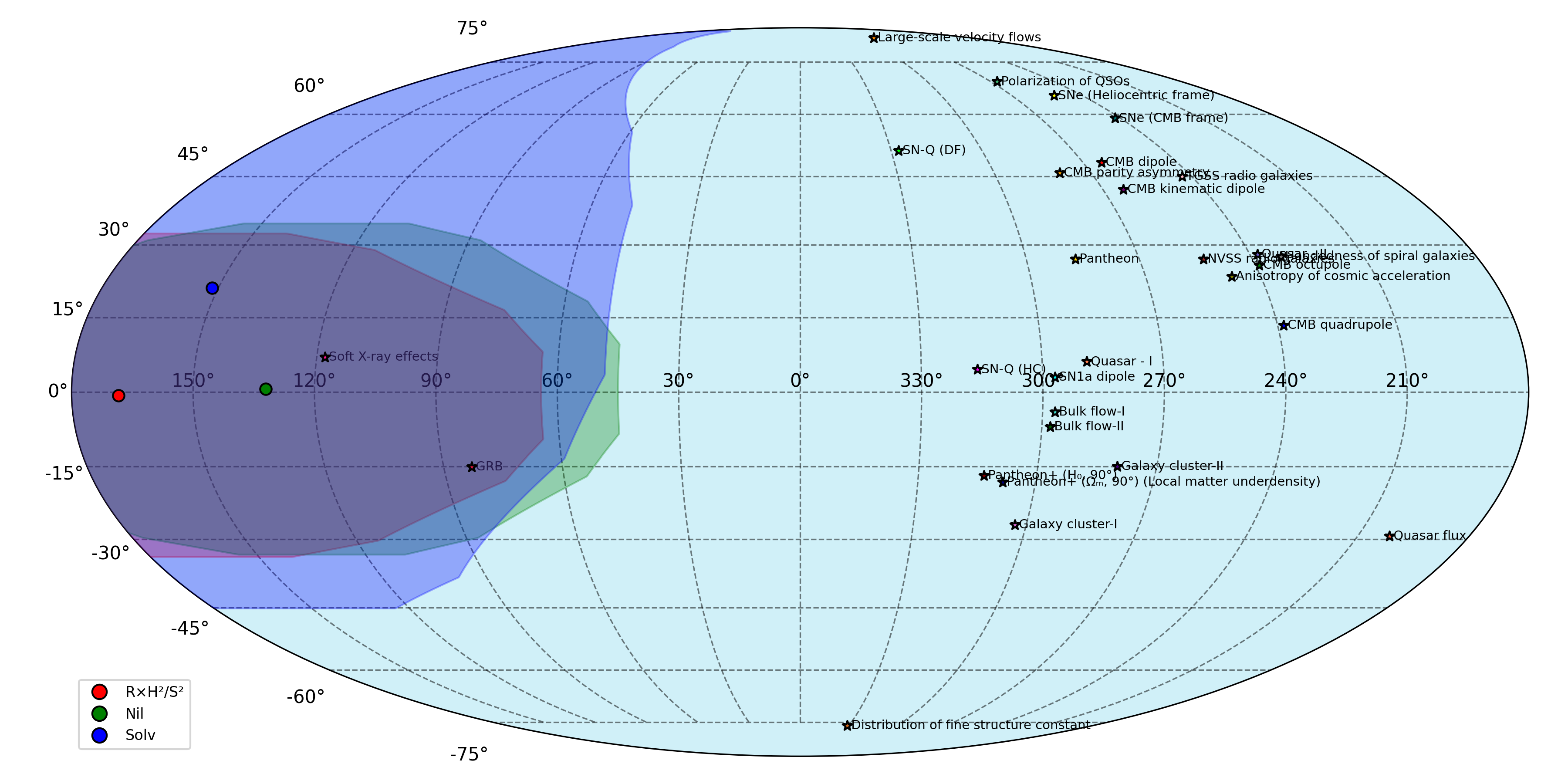
Ограничения на геометрии и карту неба демонстрируют, что при равенстве <span class="katex-eq" data-katex-display="false">\bar{w}=w\_{a}=w\_{b}</span>, существуют определенные рамки, в которых эти параметры могут изменяться, определяя допустимые конфигурации системы. — Ограничения на геометрии и карту неба демонстрируют, что при равенстве $\bar{w}=w\_{a}=w\_{b}$ , существуют определенные рамки, в которых эти параметры могут изменяться, определяя допустимые конфигурации системы.

Ограничения на анизотропные космологические модели на основе наблюдаемых данных о красном смещении и реликтовом излучении.

Наблюдаемые отклонения от изотропности Вселенной ставят под вопрос справедливость стандартной космологической модели FLRW. В работе ‘Thurston geometries and parameter constraints from SNIa data’ исследуется возможность расширения ΛCDM модели с использованием уникальных топологических пространств Тёрстона, допускающих анизотропию. Полученные ограничения на параметры моделей, основанные на данных сверхновых типа Ia (Pantheon+ \& SH0ES), указывают на слабую, но заметную вероятность нарушения изотропности в больших масштабах. Способны ли такие анизотропные геометрии Тёрстона предложить более точное описание космологической эволюции Вселенной, чем существующие модели?

Космологический принцип: от точности к сомнению

Стандартная космологическая модель, известная как ΛCDM, с удивительной точностью описывает множество наблюдаемых явлений во Вселенной, начиная от реликтового излучения и заканчивая крупномасштабной структурой. В основе её успеха лежит космологический принцип — предположение о том, что Вселенная в больших масштабах однородна и изотропна. Это означает, что Вселенная выглядит одинаково для любого наблюдателя, вне зависимости от его местоположения или направления взгляда. Однородность подразумевает, что плотность вещества во Вселенной примерно постоянна в больших масштабах, а изотропность — что свойства Вселенной одинаковы во всех направлениях. Именно эти фундаментальные предположения позволяют строить математические модели, успешно предсказывающие эволюцию Вселенной и интерпретирующие полученные астрономические данные. Успех ΛCDM модели, таким образом, тесно связан с принятием космологического принципа как базового для понимания структуры Вселенной.

Недавние астрономические наблюдения всё чаще указывают на возможные отклонения от космологического принципа, который предполагает однородность и изотропность Вселенной в больших масштабах. В частности, данные, полученные в ходе изучения космического микроволнового фона и распределения галактик, демонстрируют аномалии, которые сложно объяснить в рамках стандартной ΛCDM-модели. Эти отклонения заставляют пересматривать фундаментальные предположения о структуре Вселенной и рассматривать возможность, что наблюдаемая однородность является лишь локальным свойством, а в более крупных масштабах пространство может быть неоднородным и анизотропным. Подобные открытия стимулируют поиск альтернативных космологических моделей и новых методов анализа данных, способных учесть потенциальную неоднородность Вселенной и дать более точное описание её эволюции.

Наблюдаемые аномалии в крупномасштабной структуре Вселенной требуют пересмотра традиционных представлений о её геометрии. Если космологический принцип, постулирующий однородность и изотропность Вселенной, подвергается сомнению, то и описание её формы должно учитывать более сложные варианты. Исследователи активно изучают альтернативные геометрические модели, включая неевклидовы пространства и топологически нетривиальные конфигурации, чтобы понять, не является ли наблюдаемая Вселенная лишь частью более обширной и сложной структуры. Эти исследования включают анализ данных о космическом микроволновом фоне, распределении галактик и гравитационных линзах, что позволяет оценить, насколько хорошо различные геометрические модели соответствуют наблюдаемой реальности и могут ли они объяснить аномалии, не вписывающиеся в рамки стандартной $ΛCDM$ модели.

За пределами FLRW: геометрии Тёрстона как альтернатива

Геометрии Тёрстона представляют собой класс пространств-времен, расширяющих стандартную метрику Фридмана — Леметра — Робертсона — Уокера (FLRW), и позволяют моделировать анизотропные вселенные. В отличие от FLRW, предполагающей изотропность и однородность, геометрии Тёрстона сохраняют однородность, но допускают нарушение изотропии, то есть физические свойства могут различаться в разных направлениях. Это достигается путем использования Riemann-пространств и рассмотрения геометрий, не требующих полной симметрии относительно всех направлений. В результате, геометрии Тёрстона предоставляют теоретическую основу для исследования космологических моделей, отклоняющихся от стандартного космологического принципа, и проверки их соответствия наблюдательным данным.

Геометрии Тёрстона, построенные на основе римановых пространств, сохраняют однородность, но могут нарушать изотропность, предоставляя основу для проверки отклонений от космологического принципа. В отличие от стандартной космологической модели ФРВ, предполагающей изотропность пространства, эти геометрии допускают анизотропные вселенные, сохраняя при этом однородность — то есть, статистическую одинаковость свойств пространства в любой его точке. Это позволяет исследовать космологические модели, в которых наблюдаемая Вселенная может иметь предпочтительные направления или асимметрии, что может быть связано с физикой на самых ранних стадиях развития Вселенной или с влиянием крупномасштабных структур. Нарушение изотропии проявляется в зависимости красного смещения от направления наблюдения, что позволяет, теоретически, выявить эти отклонения посредством космологических наблюдений.

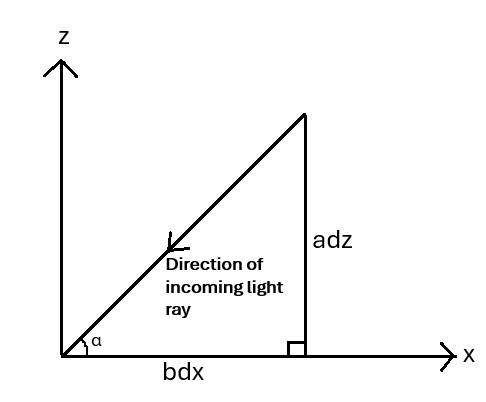
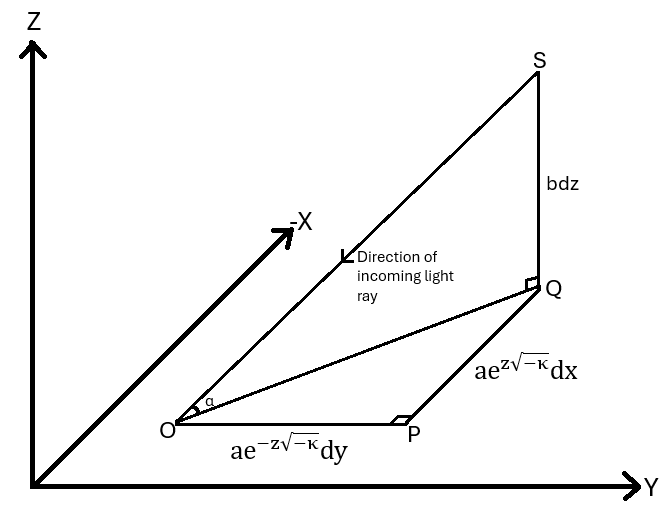
В рамках геометрий Тёрстона, геометрии Solv и Nil представляют собой конкретные примеры пространств, демонстрирующих различные свойства симметрии, отклоняющиеся от изотропности, характерной для стандартной космологической модели ФРВ. Получены уравнения для красного смещения и расстояния в пространствах $ℝ\timesℍ^2/S^2$ , Nil и Solv. Эти уравнения позволяют численно оценить отклонения от предсказаний ФРВ-метрики и служат основой для проверки космологического принципа на наблюдательных данных. Конкретно, геометрия Solv характеризуется одним направлением, вдоль которого наблюдается анизотропия, в то время как геометрия Nil демонстрирует более выраженное нарушение изотропии, проявляющееся в двух направлениях.

В пространстве-времени Ниля линия видимости определяется геометрией нулевых геодезических.

Поиск анизотропии в крупномасштабной структуре Вселенной

Если Вселенная обладает космической предпочтительной осью, это проявится в тонких корреляциях в распределении крупномасштабной структуры. Предпочтительная ось создаст анизотропию в статистических свойствах распределения галактик и других космических объектов. Наблюдаемые корреляции будут представлять собой отклонения от изотропного распределения, которое ожидается в стандартной космологической модели. Эти корреляции могут быть обнаружены путем анализа крупномасштабных обзоров галактик и квазаров, а также путем изучения поляризации космического микроволнового фона. Обнаружение таких корреляций станет сильным свидетельством в пользу анизотропии Вселенной и потребует пересмотра стандартной космологической модели.

Поляризация квазаров и радиоизлучения предоставляет методы для картирования корреляций в крупномасштабной структуре Вселенной и поиска отклонений от изотропии. Измерение поляризации электромагнитного излучения от квазаров и радиоисточников позволяет оценить выравнивание векторов поляризации на больших масштабах. В случае наличия предпочтительной оси во Вселенной, поляризационные сигналы будут демонстрировать статистически значимые корреляции, отклоняющиеся от случайного распределения. Анализ этих корреляций требует учета инструментальных эффектов и астрофизических источников поляризации, отличных от исследуемого космологического сигнала, для обеспечения высокой точности и достоверности результатов.

Для моделирования анизотропных эффектов в крупномасштабной структуре Вселенной критически важны масштабный фактор в геометрии Solv и измерение расстояния по красному смещению. Наш анализ демонстрирует, что расстояние по красному смещению в пространстве-времени Solv не зависит от параметра кривизны κ, в отличие от геометрий ℝ×ℍ²/S². Это означает, что определение расстояний до объектов в рамках SolvGeometry не подвержено систематическим ошибкам, связанным с изменением κ, что является важным преимуществом при анализе анизотропии и построении космологических моделей. Точное определение масштабного фактора и расстояний по красному смещению необходимо для корректной интерпретации наблюдаемых корреляций в распределении крупномасштабной структуры.

Линия видимости в пространстве-времени Solv демонстрирует искажение световых лучей под влиянием гравитационного поля.

Влияние на космологию и перспективы будущих исследований

Обнаружение анизотропных сигнатур в космическом микроволновом фоне (CMB) стало бы серьезным вызовом для космологического принципа — фундаментального допущения современной космологии, утверждающего однородность и изотропность Вселенной в больших масштабах. В случае подтверждения анизотропии, существующие космологические модели, основанные на предположении изотропности, потребуют пересмотра. Необходимо будет разработать и исследовать альтернативные модели, учитывающие анизотропные геометрии и позволяющие описать наблюдаемые отклонения от изотропности. Это подразумевает переход к более сложным математическим описаниям Вселенной, в которых различные направления в пространстве обладают различными физическими свойствами, что, в свою очередь, потребует переосмысления понимания эволюции и структуры Вселенной.

В случае обнаружения анизотропных сигнатур, существующее понимание космического микроволнового фона (CMB) потребует пересмотра. Традиционно, анализ CMB основывается на предположении об изотропности Вселенной, что значительно упрощает интерпретацию наблюдаемых флуктуаций температуры. Однако, если Вселенная не является однородной и изотропной, а характеризуется анизотропной геометрией, то наблюдаемые анизотропии CMB будут не просто отражением ранних флуктуаций плотности, а также результатом искажений, вызванных не-евклидовой структурой пространства-времени. Это означает, что текущие методы, используемые для определения космологических параметров, таких как постоянная Хаббла и плотность темной энергии, могут давать неверные результаты, а интерпретация спектра мощности CMB потребует учета новых геометрических эффектов. Исследование анизотропных моделей потребует разработки новых теоретических инструментов и алгоритмов анализа данных, позволяющих корректно извлекать информацию о ранней Вселенной из наблюдаемых анизотропий CMB.

Дальнейшие исследования направлены на усовершенствование наблюдательных методов и разработку более сложных моделей, позволяющих точно характеризовать любые обнаруженные анизотропии и ограничивать параметры альтернативных геометрий. Предварительные оценки, установившие пределы для параметра кривизны κ и количественно оценившие анизотропию, служат прочной основой для будущих ограничений. Улучшение точности измерений космического микроволнового фона и других космологических параметров позволит проверить предсказания различных теоретических моделей и пролить свет на фундаментальные вопросы о форме и эволюции Вселенной. Особое внимание уделяется разработке новых алгоритмов обработки данных и статистических методов, способных выявлять слабые сигналы анизотропии на фоне космического шума.

Исследование геометрий Тёрстона в космологии, представленное в данной работе, неизбежно сталкивается с проблемой интерпретации наблюдательных данных. Авторы стремятся проверить, насколько анизотропные пространства, предложенные Тёрстоном, согласуются с данными о сверхновых типа Ia и космическом микроволновом фоне. Однако, как показывает практика, даже самые точные измерения могут быть подвержены влиянию субъективных оценок и неверных предположений. В связи с этим, вспоминается высказывание Иммануила Канта: «Знание начинается с опыта, но не сводится к нему». Данное исследование, стремясь установить параметры анизотропии пространства, демонстрирует, что истинное понимание Вселенной требует не только сбора данных, но и критического осмысления полученных результатов, постоянной проверки гипотез и сомнений в собственных выводах. Чем сложнее модель, тем больше возможностей для искажения реальности.

Что дальше?

Представленная работа, исследующая возможности неизотропных космологических моделей, основанных на геометриях Тёрстона, неизбежно сталкивается с фундаментальной проблемой: выборка данных — это всегда лишь мнение реальности, и никакая, даже самая обширная, не способна охватить всю сложность космоса. Ограничения, накладываемые данными о сверхновых типа Ia и космическом микроволновом фоне, предоставляют лишь частичную картину, а истинные отклонения от изотропности могут скрываться за пределами текущей точности измерений. Необходимо помнить, что «дьявол не в деталях — он в выбросах», и именно аномалии могут указать на новые физические явления.

Будущие исследования должны сосредоточиться не только на уточнении параметров существующих моделей, но и на разработке новых методов анализа данных, способных выявлять тонкие асимметрии и отклонения от стандартной космологической модели. Особое внимание следует уделить комбинированию данных из различных источников — гравитационных волн, крупномасштабной структуры Вселенной — с целью получения более полной и непротиворечивой картины. Важно не забывать, что средние значения часто маскируют важные детали, и анализ разброса данных может оказаться более информативным.

В конечном итоге, поиск истины в космологии — это непрерывный процесс проб и ошибок, сомнений и переоценок. Истинное понимание Вселенной потребует не только математической элегантности моделей, но и готовности отказаться от устоявшихся представлений, когда этого потребуют данные. Именно в этом парадоксе и заключается красота научного поиска.

Оригинал статьи: https://arxiv.org/pdf/2602.02936.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-02-04 10:36